faire des paires de rectangles sur deux surfaces différentes

Bonjour !

Mon problème est peut être un peu bateau mais réel, j'enlèverais le post s'il n'a pas sa place ici.
J'ai deux planches de bois, une claire de 180 par 47 cm2 et une sombre de 150 par 58 cm2
Je veux faire des planchettes bifaces (clair et sombre) en ayant le moins de perte possible. J'ai quatre dimensions possibles, 22 par 17, 27 par 18, 33 par 18 et 17 par 15. Je voudrais connaitre le nombre de planchettes que je dois faire de chaque dimension.

Pour l'instant j'ai trouvé ces équations là, mais je n'arrive pas à en faire grand chose, je n'ai pas les connaissances pour, et je ne peux pas me contenter des aires :
$22.17 a + 27.18 b + 33.18 c + 17.15 d + x = 180.47$
$22.17 a + 27.18 b + 33.18 c + 17.15 d + y = 150.58$

J'espère avoir représenté correctement les multiplications, les astérisques donnent des choses différentes.
Comment doit-on s'y prendre pour trouver a, b, c et d ?
Merci pour votre attention !

@Titus-Titus Bonjour,

Avec 6 inconnues, pour être sur de trouver une solution, il faudrait 6 équations.
Donc difficile avec 2 équations de trouver une solution.

Est-il obligatoire de faire des planchettes des quatre dimensions ?
Il faudrait peut être travailler avec les dimensions au lieu des surfaces.

Merci pour la réponse rapide !
Idéalement j'aimerais faire des planchettes des 4 dimensions mais je peux me débrouiller en n'en faisant que de 22 par 17

@Titus-Titus
Si vous utilisez les aires.
Pour la planche de bois claire
son aire est égale à $8460\ cm^2$
En prenant une seule planchette, l'aire totale est de $1709\ cm^2$
donc en théorie 4,95 planchettes de chaque dimensions.

Pour la planche sombre
aire : $8700\ cm^2$
nombre 5,09 planchettes

Mais ici c'est théorique car on ne prend pas en compte les dimension.
Il faut trouver la (ou les) disposition(s) possible(s) des planchettes par rapport à chacune des planches.

Oui, c'est ça ! J'avais essayé quelques dispositions avec des patrons en papier, puis je me suis dit que ça devait être calculable, mais je ne trouvais pas le moyen de le faire, comme vous l'avez dit, avec deux équations et 6 inconnues.

Un exemple de disposition
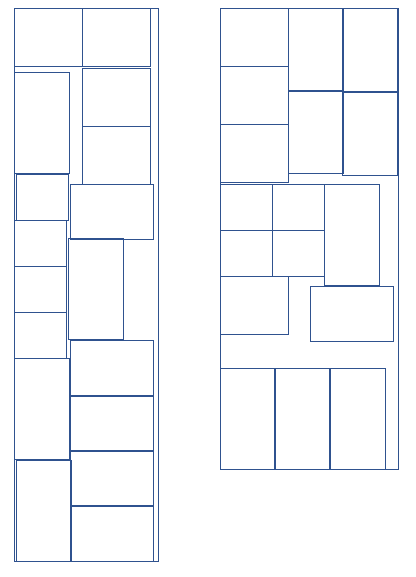
On peut noter que le nombre est compris entre 4 et 5 si on souhaite une répartition à peu prés égale de chaque planchettes.
Pour une mise en équation, il faut prendre en compte l'ensemble des dimensions donc les contraintes des longueurs et largeur de chaque objets.

Oui, cet exemple est pas mal, il y a peu de déperdition !
Vous voulez dire de plutôt chercher à exprimer les équations selon un nombre de segments ?
Par contre ça fait monter à 8 inconnues.

Tu peux utiliser un logiciel d'optimisation de coupe pour limiter les pertes.

OK ! Je vais essayé ça alors, et sinon je ferai au mieux avec des schémas. Merci beaucoup pour le temps que vous avez passé sur le sujet