Integrale pour determiner laire

J'ai du mal à résoudre ce problème, je dois le résoudre avec une double ou triple intégrale
Merci d'avance!

@Hichem-Mahammedi Bonjour (Marque de politesse à ne pas oublier !!)

L'aire : $\dfrac {1}{2}\displaystyle\int_{\alpha}^{\beta} r^2d\theta$

Bonjour,

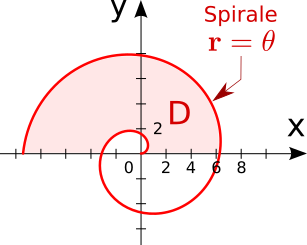
@Hichem-Mahammedi , s'agit-il de l'aire de la partie teintée du schéma joint ?
Si c'est bien le cas, tu dois faire une différence.

Soit A l'aire de la partie teintée
$A=∫2π3π12r2dθ−∫0π12r2dθ\displaystyle A=\int_{2\pi}^{3\pi}\dfrac{1}{2}r^2d\theta-\int_{0}^{\pi}\dfrac{1}{2}r^2d\theta$

Vu que $r=θr=\theta$ , le calcul est simple à faire.

Si tu souhaites une intégrale double, tu peux penser qu'un élément infinitésimal d'aire est vu comme $rdrdθrdrd\theta$

$A=∫2π3π∫0r(θ)rdrdθ−∫0π∫0r(θ)rdrdθ\displaystyle A=\int_{2\pi}^{3\pi}\int_{0}^{r(\theta)}rdrd\theta -\int_{0}^{\pi}\int_{0}^{r(\theta)}rdrd\theta$

$r(θ)=θr(\theta)=\theta$

Après calcul intégral, tu dois trouver le même résultat qu'avec la première méthode.

@Hichem-Mahammedi , après calculs, sauf erreur, tu dois trouver pour l'aire de la partie hachurée : $A=3π3A=3\pi^3$

Bons calculs.