Déterminer les dimension d'une boite - fonctions plusieurs variables
-
dounia032 dernière édition par
Bonjour, j'ai besoin d'aide pour résoudre un devoir maison, sur le thème des fonctions à plusieurs variables ?
On veut construire une boite entièrement fermée constituée de 2 parallélépipèdes rectangles ,
la plus légère possible (avec le minimum de surface possible) dont le volume du parallélépipède du bas doit être égal à V = xyz = 32/5.
Quelles doivent être ses dimensions : largeur (x), longueur (z), et hauteur (y)?
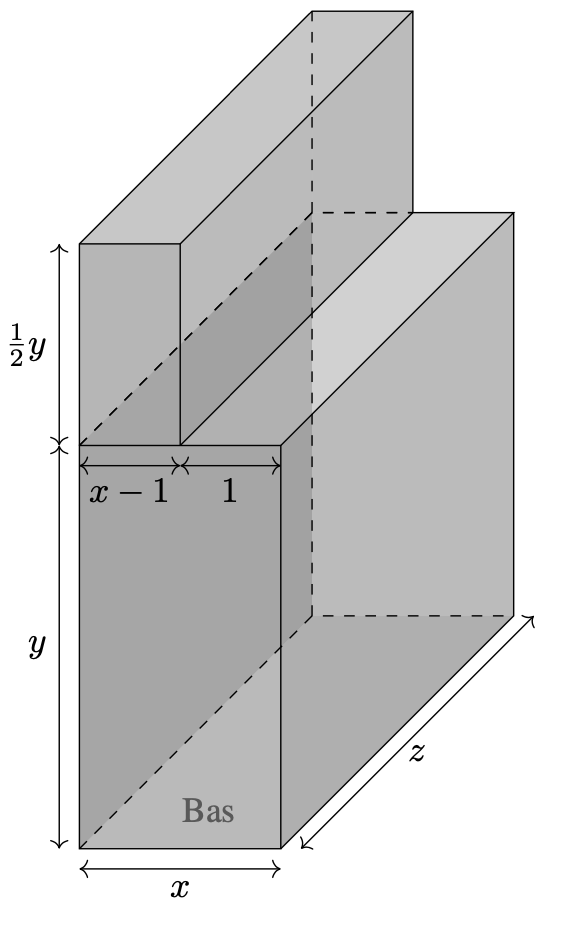
Je ne vois pas par où commencer, si quelqu'un pourrait m'aiguiller ?
-
@dounia032 Bonjour,
Commence par calculer l'aire de toutes les surfaces en fonction de xxx, yyy et zzz.
-
dounia032 dernière édition par
Bonjour, si j'ai bien compris je n'ai que deux surface en fonction de x et y donc :
. 1/2y X (x-1)
. yx
-
-
dounia032 dernière édition par
J'obtiens : ( j'ai essayé simplifier )
z(x-1) + y(x-1) + 3yz +2yx + xz + 1z
-
Tu peux encore simplifier en développant.
Tu utilises ensuite le fait que V=xyz=325V=xyz=\dfrac{32}{5}V=xyz=532
pour remplacer zzz par 325xy\dfrac{32}{5xy}5xy32puis tu écris la relation S=f(x;y)S = f(x;y)S=f(x;y)
-
dounia032 dernière édition par
En simplifiant j'ai,
2zx + 3yx + 3yz - y
en remplaçant z par 32/5 :
(64/5xy)x + 3yx + (96/5xy)y - y
Après je ne comprend pas comment écrire la relation y=f(x) ,
-
Tu peux simplifier l'expression.
Il faut ensuite chercher le minimum de cette fonction qui correspond à la surface :
S(x,y)=...S(x,y)= ...S(x,y)=...
-
dounia032 dernière édition par
j'ai : (64x + 15x^2y^2 + 96y - 5xy^2) / (5xy)
Je n'arrive pas à trouver le minimum

-
A partir du volume que peut-on dire sur les valeurs possibles pour les trois variables.
Cherche ensuite s'il existe des points critiques.
-
dounia032 dernière édition par
Je crois qu'il n'existe pas de point critique car en calculant :
.3y - 96/5x^2 = 0 (dérivé par rapport à x)
.-64/5y^2 + 3x - 1 = 0 (dérivé par rapport à y)
je n'obtient pas de vrai résultat
-
Tu peux trouver un point critique (2;8/5)
-
dounia032 dernière édition par
Je vais essayer de trouver ça demain !
merci pour aujourd'hui !
-
dounia032 dernière édition par
Re bonjour,
Je n'arrive toujours pas à trouver ce point critique, peut être que je me suis trompé dans les surfaces à prendre en compte ?
-
Résous le système, tu isoles yyy de la première équation que tu remplace dans la deuxième.
Tu obtiens une équation de degré 4 mais avec une racine évidente x=2x=2x=2.
-
dounia032 dernière édition par
j'obtiens (-5/16)x^4 + 3x - 1 = 0
Du coup je trouve bien le point critique (2;8/5) en remplaçant x=2 pour y = 96/15x^2
Il s'agit là du minimum ?
-
Il faut vérifier si c'est un minimum.
Calcule S(2;8/5)S(2;8/5)S(2;8/5).
Tu écris ensuite S(x,y)S(x,y)S(x,y) en posant u=x−2u=x-2u=x−2 et v=y−8/5v=y-8/5v=y−8/5.
-
dounia032 dernière édition par
j'ai : S(2;8/5) = 176/5
-
Je trouve 128/5.
-
dounia032 dernière édition par
Ah oui en effet je me suis trompé dans le calcul
-
dounia032 dernière édition par
donc le minimum est bien 128/5 atteint en (2;8/5)
-
Tu écris ensuite S(x,y)S(x,y)S(x,y) en posant u=x−2u=x-2u=x−2 et v=y−8/5v=y-8/5v=y−8/5.
et tu vérifies que c'est supérieur à 128/5.
-
dounia032 dernière édition par
Je ne comprend pas trop quoi faire de u et v
-
Tu remplaces sss par u+2u+2u+2 et yyy par v+8/5v+8/5v+8/5 pour montrer que :
S(x,y)≥1285S(x,y) \geq \dfrac{128}{5}S(x,y)≥5128
-
dounia032 dernière édition par
je trouve un très grand nombre
-
Sauf erreur de calcul, tu dois trouver :
645(v+8/5)+(v+8/5)(3u+5)+965(u+2)\dfrac{64}{5(v+8/5)}+(v+8/5)(3u+5)+\dfrac{96}{5(u+2)}5(v+8/5)64+(v+8/5)(3u+5)+5(u+2)96
-
dounia032 dernière édition par
Oui j'avais bien trouvé ça, j'aurais pas du autant développer
-
dounia032 dernière édition par
finalement j'obtiens une grande équation et isole seulement les nombres qui ne possède pas de u ni de v et j'ai 2048/80 qui est égale à 128/5
-
Il faut montrer que l'expression est toujours supérieure ou égale à 128/5.
-
dounia032 dernière édition par
ça peut justifier que S(x;y)>= 128/5 ?
-
dounia032 dernière édition par
Je dois faire apparaître un terme de degré 2 pour intégrer le signe >= 0 ?
-
Si possible.
-
dounia032 dernière édition par
Je suis un peu bloqué, je n'arrive pas à faire apparaître un carré car j'ai des termes différents qui ne peuvent pas s'additionner entre eux.
J'ai essayé de développer l'expression mais je vois pas comment intégrer le signe >=
-
Le cours indique t-il une autre méthode pour déterminer un minimum ?
-
dounia032 dernière édition par
Le cours évoque les formes quadratiques, cependant je n'ai pas accès à la totalité du cours car le professeur nous donne le devoir maison avant, pour nous pousser à chercher
-
Calcule les dérivées secondes.
-
dounia032 dernière édition par
Je trouve :
. 3v + (24/5) - (480/(5u+10)^2)
. (-320/(5v+8)^2) + 3u + 5
-
Calcule les dérivées secondes en partant du résultat des dérivées premières.
∂S∂x=3y−965x2\dfrac{\partial{S}}{\partial{x}}=3y-\dfrac{96}{5x^2}∂x∂S=3y−5x296∂2S∂x2=1925x3\dfrac{\partial^2{S}}{\partial{x^2}}=\dfrac{192}{5x^3}∂x2∂2S=5x3192
∂S∂y=3x−645y2−1\dfrac{\partial{S}}{\partial{y}}=3x-\dfrac{64}{5y^2}-1∂y∂S=3x−5y264−1
∂2S∂y2=1285y3\dfrac{\partial^2{S}}{\partial{y^2}}=\dfrac{128}{5y^3}∂y2∂2S=5y3128
∂2S∂x∂y=3\dfrac{\partial^2{S}}{\partial{x}\partial{y}}=3∂x∂y∂2S=3
-
dounia032 dernière édition par
par rapport à y j'ai :
. 128/5y^3
-
Oui, j'ai indiqué les résultats.
calcule ensuite h(2;8/5)h(2;8/5)h(2;8/5)
et
∂2S∂x2(2;8/5)\dfrac{\partial^2 S}{\partial{x^2}}(2;8/5)∂x2∂2S(2;8/5)
-
dounia032 dernière édition par
∂^2S/∂x^2 (2;8/5) = 24/5
Je ne vois pas à quelle fonction correspond h
-
h(x,y)=∂2S∂x2(x,y)×∂2S∂y2(x,y)−(∂2S∂x∂y(x,y))2h(x,y)=\dfrac{\partial^2S}{\partial{x^2}}(x,y)\times \dfrac{\partial^2S}{\partial{y^2}}(x,y)-(\dfrac{\partial^2S}{\partial{x}\partial{y}}(x,y))^2h(x,y)=∂x2∂2S(x,y)×∂y2∂2S(x,y)−(∂x∂y∂2S(x,y))2
-
dounia032 dernière édition par
cela fait : h(2;8/5) = 24/5 x 25/4 - 3 = 21
-
Le résultat est juste, tu as oublier le carré pour 3.
Comme h(2,8/5)h(2,8/5)h(2,8/5) et ∂2S∂x2\dfrac{\partial ^2S}{\partial{x^2}}∂x2∂2S sont supérieur à 0, alors S(2,8/5)S(2,8/5)S(2,8/5)est un minimum.
Tu conclus x=2x=2x=2, y=8/5y=8/5y=8/5, z=2z=2z=2.
-
dounia032 dernière édition par
J'ai tout compris !
Je vous remercie beaucoup d'avoir pris le temps de m'aider !
-
J'espère que tu as tout compris.
-
dounia032 dernière édition par
Oui c'était très clair
-