Devoir probabilité interférence Bayésienne

Ce message a été supprimé !

Ce message a été supprimé !

REMARQUE de @mtschoon :
Vu que l'énoncé a été supprimé (ainsi que les questions intermédiaires) par l'utilisateur, ce qui fait perdre tout son sens à l'exercice, pour consultation éventuelle, énoncé/solutions sont en fin de topic.

Ce message a été supprimé !

@Alexis-Dedigama

OK pour l'arbre.

Si je suis arrivée à bien lire ta réponse de la partie 2 , cela est exact.

Mais du coup je ne trouve pas réellement de valeur, est-ce normal ?

Ce message a été supprimé !

@Alexis-Dedigama

La première ligne que tu indiques est bonne, mais ta simplification ne l'est pas.
Vu que tu ne connais pas p, tu ne peux trouver qu'une expression en fonction de p. C'est d'alleurs indiqué dans ton énoncé.

Tu peux développer le dénominateur pour réduire une peu l'expression.

$0.95p0.95p+0.35−0.35p=0.95p0.6p+0.35\dfrac{0.95p}{0.95p+0.35-0.35p}=\dfrac{0.95p}{0.6p+0.35}$

Ce message a été supprimé !

@Alexis-Dedigama ,

Oui, vu que l'énoncé ne te donne pas la valeur de p, tu ne peux pas faire mieux.

Ce message a été supprimé !

@Alexis-Dedigama , as-tu répondu en totalité à la patir 2 ?

Dans ton énoncé , tu as écrit
Calculer, en fonction de 𝑝, 𝑃𝐶𝑇𝐹(𝐺)''P(G) sachant CTF)'' et 𝑃𝐶𝑇𝐹(𝐺̅ barre) ''P(G barre) sachant CTF''.
Comme déjà dit, c'est peu comprésensible...mais j'ai l'impression qu'il y a deux probabilités à calculer..

Tu as calculé $pCTF(G)\boxed{p_{CTF}(G)}$ c'est à dire probabilité de G sachant CTF.
Est-ce la seule probabilité à calculer ?

Tu devrais vérifier.

Pour la suite,
pour la partie 3, il faut prendre p=0.7 , calculer l'expression trouvée à l'étape 2 et tirer la conclusion.

pour la partie 4, il faut prendre p=0.2 et faire pareil.

Ce message a été supprimé !

Du coup pour la partie 3 et 4 vous m’avez dit de reprendre l’expression calculer à l’étape 2. Mais c’est quel expression que je reprends car j’en ai 2 du coup

@Alexis-Dedigama ,

OK pour $pCTF(G‾)p_{CTF}(\overline {G})$ .

Tu peux simplifier un peu le dénominateur.

Tu peux remarquer que ces deux évènements $G$ sachant CTF et $G‾\overline{G}$ sachant CTF sont contraires l'un de l'autre.

Tu peux vérifier que

$pCTFG‾=1−pCTF(G)p_{CTF}\overline{G}=1-p_{CTF}(G)$

Pour 3) et 4) , relis bien l'énoncé.

Sachant que Mr Condriac à C,T et F (évènement CTF) , le médecin a dignostiqué une grippe (évènement G).

La probabilité de réussite du diagnostic du médecin est la valeur de $p_{CTF}(G)$

La probabilité d'erreur du diagnostic du médecin est la valeur de $pCTF(G‾)p_{CTF}(\overline{G})$

Ce message a été supprimé !

@Alexis-Dedigama ,

Relis l'énoncé,
Les questions s'enchaînent. Elles ne sont pas indépendantes.
Les données des parties 1 et 2 sont à utiliser pour les parties 3 et 4.
En bref, les parties 3 et 4 sont les applications numériques des parties 1et 2.

Dans la modélisation, il est écrit :
on note 𝑝 la probabilité que le patient ait la grippe.
donc, 1-p est la probabilité pour que le patient n'ait pas la grippe.

Dans la 3), p=0.7, donc $1 - p = 1 - 0.7 = 0.3$

Dans la 4), p=0.2, donc $1 - p = 1 - 0.2 = 0.8$

Vu que les formules du 2) sont en fonction de p, c'est plus simple de remplacer p par sa valeur, que d'utiliser 1-p.

Ce message a été supprimé !

@Alexis-Dedigama ,

Oui.

@Alexis-Dedigama , re-bonjour,

Pour la 4), p=0.2 et tu ne dois pas avoir de difficulté pour le calcul (même principe que pour la 3) ).

Pour justifier l'évolution du risque d’erreur du médecin, si tu veux faire une justification soignée, tu peux étudier les variations de la foction f définie par $f(p)=0.35−0.35p0.6p+0.35f(p)=\dfrac{0.35-0.35p}{0.6p+0.35}$ pour $p∈[0,1]p\in [0,1]$
Tu trouveras $f′(p)<0f'(p)\lt 0$ donc f strictement décroissante. et tu tireras la concluson :
Plus l'épidémie de grippe diminue ( p diminue ), plus le risque d'erreur du médecin augmente ( f(t) augmente ).

Reposte si besoin.
Bon travail.

Ce message a été supprimé !

@Alexis-Dedigama ,

Ce que j'ai appellé $f (p)$ c'est la probabilité de $G‾\overline{G}$ sachant CTF, qui vaut $0.35−0,35p0.6p+0.35\dfrac{0.35-0,35p}{0.6p+0.35}$

f est une fonction de la variable p
p varie de 0 à 1, vu que c'est une probabilité.
Comme déjà indiqué, tu peux étudier les variations de cette fonction f et tirer la conclusion souhaitée.

Remarque : si la notation $p$ te gène pour l'étude d'une fonction , tu remplaces $p$ par $x$ (avec $x$ variant de 0 à 1) et tu poses :
$f(x)=0.35−0.35x0.6x+0.35f(x)=\dfrac{0.35-0.35x}{0.6x+0.35}$

Ce message a été supprimé !

@Alexis-Dedigama , il me semble voir quelque chose de pas clair au numérateur de f'(x), qui engendre une erreur de signe.

$U^{'} (x) = - 0.35$

Tu modifies ainsi f'(x) et tu dois trouver des simplifications au numérateur (après avoir développé).

Ce message a été supprimé !

Ce message a été supprimé !

@Alexis-Dedigama ,@Romain-Lavocat

Re-bonjour,

Il y a une erreur de signe au numérateur de la dérivée

Tu aurais dû avoir une simplification entre -0.21t et +0.21t.

Revois les signes.

Ainsi, le numérateur est strictement négatif
Vu ue le dénominateur est strictement positif (car carré non nul), la dérivée est strictement négative donc la fonction strictement décroissante.

Ce message a été supprimé !

Le numérateur de la dérivée doit être

$−0.35×(0.6p+0.35)−(0.35−0.35p)×0.6-0.35\times(0.6p+0.35)-(0.35-0.35p)\times 0.6$

Distribue avec soin sachant que , pour la multiplication,
-par -donne +

Cela fait donc :

$- 0.21 p - 0.1225 - 0.21 + 0.21 p$

Je regarde ta phrase :
Il y a un moins devant la parenthèse, je dois changer tout les signes ?
Je réponds OUI
S'il y a un moins devant une parenthèse, le moins doit s'appliquer à chaque terme entre les parenthèses.
exemple
$−(a−b)×c=(−a+b)×c=−ac+bc-(a-b)\times c=(-a+b)\times c=-ac+bc$

Ce message a été supprimé !

De rien @Alexis-Dedigama ,

J'espère que tu as compris ton problème de signe.

Ce message a été supprimé !

C'est parfait si maintenant tu as compris , car ça t'évitera des erreurs dans bien d'autres exercices.

Bon travail !

@Enoncé et tout dialogue supprimé après avoir obtenu toutes les aides demandées...

Vraiment dommage...

Bonjour,

Pour consultaion éventuelle,

Vu que les suppressions ont fait perdre à cet exercice tout son sens, je fais une synthèse rapide de l'énoncé/solutions.

ENONCE abrégé :
En épidémie de grippe, un médecin se base sur des symptômes (C(courbatures),T(maux de têtes), F(fièvre)) pour faire son diagnostic, mais il peut se tromper.
Le médecin a constaté que parmi les malades ayant les symptôtes (CTF) , 95% ont une vraie Grippe (G), et seulement 35% n'ont pas une vraie Grippe (nonG) mais seulement des états grippaux.
Mr Condriac vient voir son médecin avec les symptômes (CTF)
Le médecin diagnostique une grippe (G) pour Mr Condriac.

Le but de l'exercice est de déterminer la probabilité que le médecin fasse un faux diadnostic.

Modélisation.
Faire un arbre pondéré de la situation, avec $p$ pour probabilité de l'évènement : "le patient a la grippe (G)".
Calculer les probabilités de $G$ et de $G‾\overline{G}$ sachant que le patient a les symptômes $C T F$
On admet que 70% des patients ont la grippe (G)
Estimer la probabilité d'erreur du médecin par rapport au dignostic réalisé ( arrondi au millième)
Le pourcentage des patients ayant la grippe descend à 20%.
Comment évolue le risque d'erreur du médecin ?.

SOLUTIONS abrégées.

1 ) Arbre pondéré, avec la notation $nonG=G‾nonG=\overline{G}$

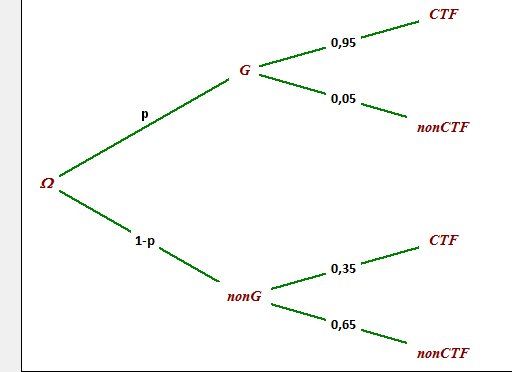
2 ) $pCTF(G)=p(G∩CTF)p(CTF)=0.95p0.95p+(1−p)0.65p_{CTF}(G)=\dfrac{p(G\cap CTF)}{p(CTF)}=\dfrac{0.95p}{0.95p+(1-p)0.65}$

$pCTF(G)=0.95p0.6p+0.35p_{CTF}(G)=\dfrac{0.95p}{0.6p+0.35}$

Pour $pCTF(G‾)p_{CTF}(\overline{G})$ , on utilise le même principe ou on passe par l'évènement contraire.

On trouve $pCTF(G‾)=(1−p)0.350.6p+0.35p_{CTF}(\overline{G})=\dfrac{(1-p)0.35}{0.6p+0.35}$

3 ) $p = 0.7$
La probabilité d'erreur du diagnostic du médecin est la valeur de $pCTF(G‾)p_{CTF}(\overline{G})$

On compte et on doit trouver
$pCTF(G‾)≈0.136p_{CTF}(\overline{G})\approx 0.136$

4 ) Même principe pour $p = 0.2$
On compte et on doit trouver
$pCTF(G‾)≈0.596p_{CTF}(\overline{G})\approx 0.596$

Pour justifier l'évolution du risque d'erreur de diagnostic du médecin, on peut étudier, pour $p∈[0,1]p\in[0,1]$ , les varitions de la fonction f définie par :
$f(p)=(1−p)0.350.6p+0.35f(p)=\dfrac{(1-p)0.35}{0.6p+0.35}$
On doit trouver cette fonction f strictement décroissante, donc plus l'épidémie de grippe diminue (p diminue), plus le risque d'erreur du médecin augmente (f(t) augmente).

Bonne lecture éventuelle.