DM MPSI fonction et polynôme

Bonjour,
Je viens aujourd'hui vers vous à propos d'un exercice de DM qui me pose problème. Voici les questions concernées. Merci par avance pour votre aide.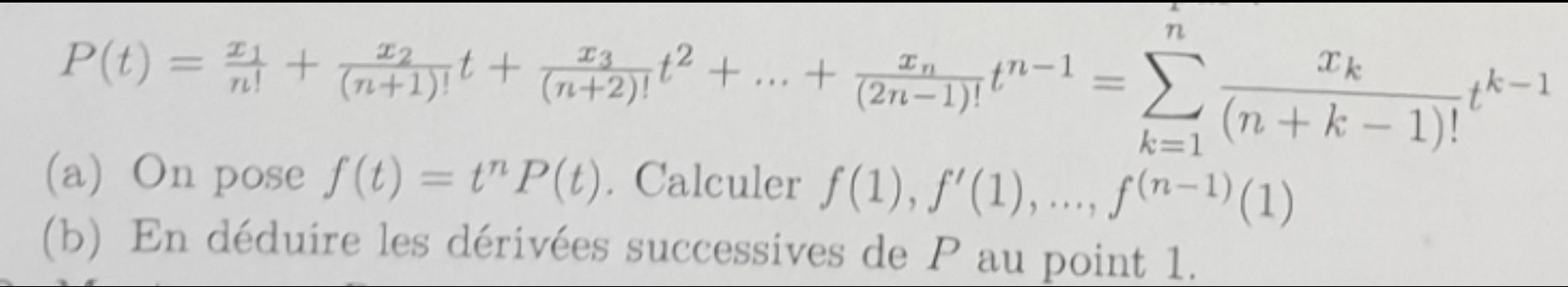

Pour la première question, s'agit-il de trouver une formule générale des dérivées en 1 (en donnant la dérivée ième) ? Et je pensais utiliser la formule de Leibniz mais la question b me fait penser que ce n'est pas adapté. Je ne sais donc que faire ici...

Je vous remercie encore par avance.
Une élève qui a besoin d'aide.

@Aline Bonjour,

Pour la question (a), exprime chaque terme en fonction de $P (1)$ et des dérivées successives de $P (1)$ .

@Noemi faut-il faire la formule de Leibniz? et dois-je prendre directement en 1 ou trouver les dérivées en t en générale et les calculer en 1?

@Aline

Calcule les dérivées successives puis écris l'expression correspondante pour $t = 1$ .

@Noemi désolée mais donc j'utilise la formule de Leibniz?

@Aline

$f(1)= 1^nP(1)= P(1)$
$f'(t)=nt^{n-1}P(t)+t^nP'(t)$
$f^{'} (1) = n P (1) + P^{'} (1)$
$f^{''} (t) = . . . .$

Bonjour,

@Aline , je ne vois pas l'intérêt de la formule de Leibniz pour la première question vu que tu as à dériver le produit d'une constante par une fonction.

Piste possible,

Tu multiplies d'abord $P (t)$ par $t^n$

$f(t)=∑k=1nxk(n+k−1)!tk−1+n\displaystyle f(t)=\sum_{k=1}^{n}\dfrac{x_k}{(n+k-1)!}t^{k-1+n}$

$f(t)=∑k=1nxk(n+k−1)!tn+k−1f(t)=\displaystyle\sum_{k=1}^{n}\dfrac{x_k}{(n+k-1)!}t^{n+k-1}$

$f(1)(t)=∑k=1nxk(n+k−1)!(n+k−1)tn+k−2f^{(1)}(t)=\displaystyle\sum_{k=1}^{n}\dfrac{x_k}{(n+k-1)!}(n+k-1) t^{n+k-2}$

$f(1)(t)=∑k=1nxk(n+k−2)!tn+k−2f^{(1)}(t)=\displaystyle\sum_{k=1}^{n}\dfrac{x_k}{(n+k-2)!} t^{n+k-2}$

Ensuite , tu trouves

$f(2)(t)=∑k=1nxk(n+k−3)!tn+k−3f^{(2)}(t)=\displaystyle\sum_{k=1}^{n}\dfrac{x_k}{(n+k-3)!} t^{n+k-3}$

Tu continues.

D'où

$f(1)=∑k=1nxk(n+k−1)!f(1)=\displaystyle\sum_{k=1}^{n}\dfrac{x_k}{(n+k-1)!}$

$f(1)(1)=∑k=1nxk(n+k−2)!f^{(1)}(1)=\displaystyle\sum_{k=1}^{n}\dfrac{x_k}{(n+k-2)!}$

$f(2)(t)=∑k=1nxk(n+k−3)!f^{(2)}(t)=\displaystyle\sum_{k=1}^{n}\dfrac{x_k}{(n+k-3)!}$

Tu continues.

Bonjour @Noemi ,

Pour la première question, j'ai proposé un calcul sans les dérivées de P(t), car on ne les connait pas et qu'elles sont demandées à la seconde question (il faut les "déduire");

@Aline verra ce qu'elle souhaite

Je pense qu'elle pourra se servir de ta piste pour la seconde question (lorsqu'elle aura fait la première)