Dérivation et tangentes

[I.swan]

Bonsoir,

Ça fait plusieurs heures que je traîne sur mon dm sans comprendre vraiment où j'ai faux et pourquoi je ne trouve pas un résultat cohérent
Le sujet est :
Montrer que les paraboles P1 d’équation y = 2x² + 2x – 3 et P2 d’équation y = - x² + 6x – 7 admettent deux
tangentes communes bien qu’elles n’admettent aucun point commun.
Déterminer l’équation réduite de chacune de ces tangentes

Alors oui la question paraît simple mais je ne sais pas pourquoi je bloque
Si quelqu'un pense connaître la piste à suivre je serai plus que reconnaissante qu'il me la partage !

Merci d'avoir pris ce temps
I.swan :))

[mtschoon]

@I-swan , bonjour,

Piste pour démarrer,

Soit $f(x)=2x^2+2x-3$ et $g(x)=-x^2+6x-7$

Soit A un point de (P1) et B un point de (P2) pour lesquels les tangentes (T1) à (P1) et (T2) à (P2) sont confondues.

Tu écris les équations de (T1) et de (T2) et tu procèdes par identification vu que (T1) et (T2) sont la même droite.

$A(a,f(a))$
$B(b,g(b))$

$(T1):y=f^{\prime }(a)(x-a)+f(a)$ tu explicites
$(T2):y=g^{\prime }(b))(x-b)+g(b)$ tu explicites

Vu que (T1) et (T2) sont confondues, tu obtiendras un système de deux équations à deux inconnues a et b à résoudre.

Donne les avancées de tes calculs/réponses pour vérification si tu le souhaites. Tu dois trouver deux cas solutions

[mtschoon]

@I-swan ,
Je t'indique une illustration graphique de l'exercice

La parabole (P1) d'équation $y=2x^2+2x-3$ est en rouge
La parabole (P2) d'équation $y=-x^2+6x-7$ est en bleu
La tangente commune (D) d'équation $y=2x-3$ est en vert
La tangente commune ($\Delta$) d'équation $y=\frac{22}{3}x-\frac{59}{9}$ est en orange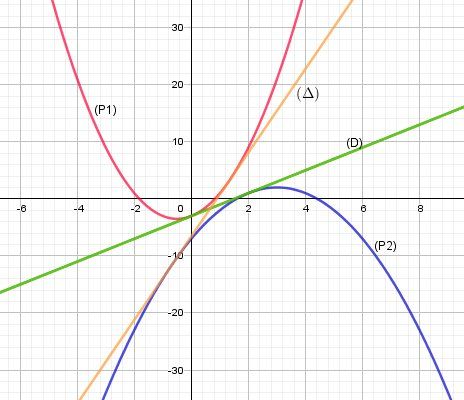

Tu peux compléter le graphique en indiquant les points de contact.

Bons calculs et reposte si besoin.