Problème avec minimisation de coût

Bonjour!
J'ai comme problème le suivant : "La fonction de coût suivante représente les frais de blanchisserie d'un hôtel: C : q^2/(q-1)^2 pour q >1"
Pour quelle quantité q de linge ce coût est-il minimum ?
J'imagine qu'il faille dériver, poser à 0 pour trouver une limite. Puis, la dérivée de second-ordre pour vérifier que ce soit bien un minimum... Je bloque juste dans mon processus de dérivation
Merci d'avance.

@Rémy-E , bonjour,

Je regarde ton énoncé.
@Rémy-E a dit dans Problème avec minimisation de coût :

"La fonction de coût suivante représente les frais de blanchisserie d'un hôtel: C : q^2/(q-1)^2 pour q >1"
Pour quelle quantité q de linge ce coût est-il minimum ?
J'imagine qu'il faille dériver, poser à 0 pour trouver une limite. Puis, la dérivée de second-ordre pour vérifier que ce soit bien un minimum... Je bloque juste dans mon processus de dérivation

Il faut que tu étudies les variations de C pour $q∈]1,+∞[q\in]1,+\infty[$

Pour cela, tu calcules la dérivée et tu trouves son signe.

Si c'est le calcul de la dérivée qui te pose problème, je te rappelle la méthode.

Si j'ai bien lu :
$C(q)=q2(q−1)2C(q)=\dfrac{q^2}{(q-1)^2}$

Rappel de la dérivée d'un quotient :
$(UV)′=U′V−UV′V2\biggr(\dfrac{U}{V}\biggr)'=\dfrac{U'V-UV'}{V^2}$

Tu poses
$U=q^2$ donc $U^{'} = 2 q$
$V=(q-1)^2$ donc $V′=2(q−1)×1=2(q−1)V'=2(q-1)\times 1=2(q-1)$

$C′(q)=2q(q−1)2−2(q−1)q2(q−1)4C'(q)=\dfrac{2q(q-1)^2-2(q-1)q^2}{(q-1)^4}$

Tu peux mettre $(q - 1)$ en facteur au numérateur

$C′(q)=(q−1)(2q(q−1)−2q2)(q−1)4C'(q)=\dfrac{(q-1)\biggr(2q(q-1)-2q^2\biggr)}{(q-1)^4}$

Je te laisse poursuivre :
Tu simplifies par $(q - 1)$
Tu développes et simplifies le numérateur restant.
Tu dois trouver au final :
$C′(q)=−2q(q−1)3C'(q)=\dfrac{-2q}{(q-1)^3}$

Bons caluls et reposte si besoin.

@mtschoon Super merci!
Et là je pose donc la dérivée =0 Ensuite on trouve 1 qui est exclu des réponses possibles puisque strictement >1. Mais comment arriver à 3 ?

@Rémy-E ,
Qu'est ce que c'est ce 3 ?

Dans ton exercice, si l'expression que tu as donnée pour $C (q)$ est vraiment la bonne (?) , la dérivée ne s'annule pas .

$q>1q\gt 1$ donc $−2q<0-2q\lt 0$ et $(x−1)3>0(x-1)^3\gt 0$ donc $C′(q)<0C'(q)\lt 0$

La fonction C est strictement décroissante.
(tu peux vérifier en faisant la représentation graphique sur ta calculette)

Le minimum est lorsque q tend vers $+∞+\infty$ , et ce minimum est 1, vu que, si tu calcules la limite :
$lim⁡q→+∞C(q)=1\displaystyle \lim_{q\to +\infty}C(q)=1$

Remarque : si tu as une réponse prévue qui te dit que le minimum est pour q=3, il faudrait que la dérivée s'annule pour q=3, ce qui n'est pas le cas.

Il y a donc une erreur dans l'expression de C(q) donnée ici.

Vérifie.

@mtschoon Je suis navré… tu as raison, c'était effectivement q^3/(q-1)^2 pour q>1

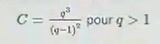
J'ai reçu des photos de la part d'un ami qui est dans une année supérieure que moi, et la qualité des photos envoyées est médiocre je ne sais si tu pourrais me modifier cela dans tes calculs précédents sans que cela te prenne trop de temps...
Merci

Cette fois, ça marche.

Je préfère que tu fasses le calcul toi même pour t'entraîner avec la méthode que je t'ai donnée .

Recopier un calcul tout fait n'est pas efficace pour s'entraîner...

Avec $C(q)=q3(q−1)2C(q)=\dfrac{q^3}{(q-1)^2}$ , tu dois trouver :
$C′(q)=q3−3q2(q−1)3=q2(q−3)(q−1)3C'(q)=\dfrac{q^3-3q^2}{(q-1)^3}=\dfrac{q^2(q-3)}{(q-1)^3}$

Bien sûr, si tu n'y arrives pas, donne tes calculs pour vérification.

@mtschoon
Je trouve donc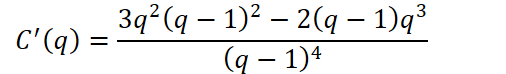

J'ai suivi la méthode donnée tout à l'heure ? Cela joue pour toi ?C^′ (q)=(3q^2 (q−1)^2−2(q−1) q^3)/(q−1)^4

@Rémy-E ,

Ce que tu as trouvé est bon.

Continue, avec le principe donné.

Tu mets $(q - 1$ ) en facteur au numérateur
Tu simplifies le quotient par $(q - 1)$
Tu développes et simplifies le numérateur ainsi trouvé , ce qui te donnera :
$C′(q)=q3−3q2(q−1)3C'(q)=\dfrac{q^3-3q^2}{(q-1)^3}$
Ensuite, au numérateur, tu mets $q^2$ en facteur , d'où la réponse :

$C′(q)=q2(q−3)(q−1)3\boxed{C'(q)=\dfrac{q^2(q-3)}{(q-1)^3}}$

Tu dois trouver :
$\lt 0$ pour $1<q<31\lt q\lt 3$
$C^{'} (q) = 0$ pour $q = 3$
$\gt 0$ pour $q>3q\gt 3$

Le côut minimum est pour $q = 3$ (et ce côut est $6, 75$ (€ ? )

Reposte si tu n'y arrives pas.