Déterminer une aire minimale, seconde.
-
44loiss dernière édition par
Bonsoir,
Je suis en seconde et ma prof de maths nous a donné un problème à résoudre. Voici l’exo :
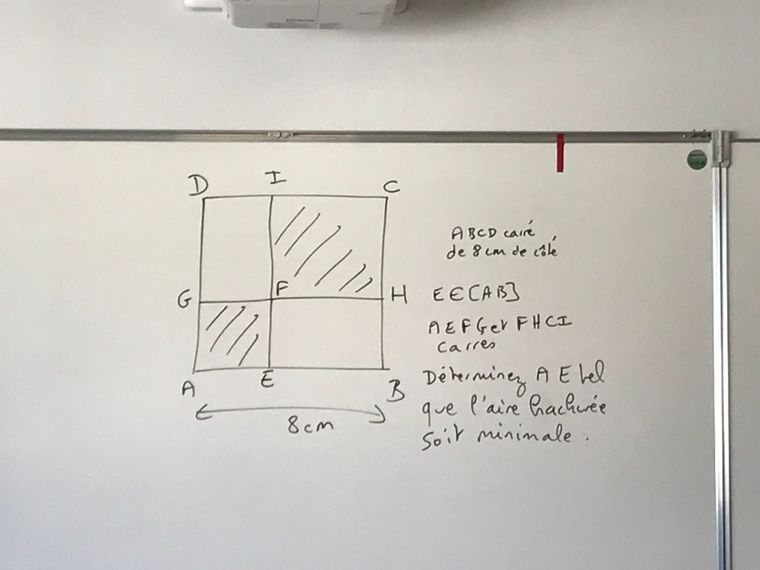
J’ai commencé par appeler x le côté [AE], puis j’ai encadré A tel que 8 > A > 0.
J’ai ensuite cherché A hachurée = A AEFG + A FHCI
J’ai obtenu x^2 + (8-x)^2 = 2x^2 - 16x + 64Et après je tourne en rond, j’ai factorisé l’expression (= 2(x^2 - 8x + 32)), puis j’ai voulu faire A hachurée > 0, j’ai tenté de conjecturer un minimum, mais tout cela me semble incorrect. De plus, en ce moment nous travaillons sur les tableaux de signes, mais je ne pense pas que ce soit ça puisqu’on cherche une aire minimale.
Pouvez vous m’aider ? Merci !
-
BBlack-Jack dernière édition par
@4loiss a dit dans Déterminer une aire minimale, seconde. :
2x^2 - 16x + 64
Bonjour,
2x^2 - 16x + 64
= 2 * [(x-4)² + 16]
... qui sera minimum quand (x-4)² sera nul ... et donc pour x = 4