Trouver l'équation de cercle

Bonsoir svp aider moi à trouver l'équation de cercle avec c'est points A (1,4) B(7,5) C(1,8)

J'imagine que tu travailles dans le plan muni d'un repère orthonormé.

Il y a différentes façons de pratiquer.

Je t'en indique une.

Une équation d'un cercle (c) de centre $I (a, b)$ et de rayon $r$ est :
$x-a)^2+(y-b)^2=r^2$
En développant, tu peux l'écrire :
$x2+y2−2ax−2by+(a2+b2−r2)=0\boxed{x^2+y^2-2ax-2by+(a^2+b^2-r^2)=0}$

Dans cette équation,
$\in (c)$ : tu peux remplacer x par 1 et y par 4
$\in (c)$ : , tu peux remplacer x par 7 et y par 5
$\in (c)$ :, tu peux remplacer x par 1 et y par 8

Tu obtiens ainsi un système de 3 équations à 3 inconnues $(a, b, r)$ à résoudre.

@MEROUA-JUDE , je t'indique quelques pistes de calculs utilisant la méthode indiquée :
Tu dois obtenir le système :
$(3)\begin{cases}17-2a-8b+a^2+b^2-r^2=0\ \ (1)\cr 74-14a-10b+a^2+b^2-r^2=0\ \ (2)\cr 65-2a-16b+a^2+b^2-r^2=0\ \ (3)\end{cases}$

(1)-(2) te donne $- 57 + 12 a + 2 b = 0$
(1)-(3) te donne $- 48 + 8 b = 0$

Tu en déduis $b = 6$ et $a = 3.75$
En substitutant dans une des 3 équations, tu dois trouver $r2=18516=11.5625r^2=\dfrac{185}{16}=11.5625$

d'où équation du cercle :
$(x−3.75)2+(y−6)2=11.5625\boxed{(x-3.75)^2+(y-6)^2=11.5625}$

Bons calculs.
Reposte si besoin ou si tu veux d'autres méthodes.

Bonjour,

Méthode alternative.

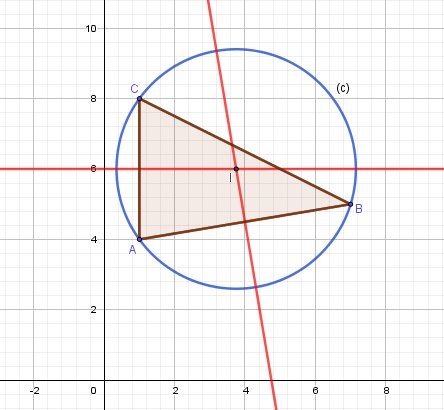
Le centre du cercle est l'intersection des médiatrices de [AC] et de [AB]

L'équation de la médiatrice de [AC] est immédiate (je te laisse voir pourquoi), c'est y = 6

Coeff directeur de (AB) : m1 = (5-4)/(7-1) = 1/6
Coeff directeur des perpendiculaires à (AB) = m2 = -1/m1 = -6
Point milieu de [AB] : M(4 ; 4,5)
Eq de la médiatrice de (AB) : y = -6x + 28,5
--> centre du cercle de coordonnées((6-28,5)/(-6) + 28,5 ; 6), soit (3,75 ; 6)

R² = |A à centre|² = (3,75-1)² + (6 - 4)² = 11,5625

Eq du cercle : (x - 3,75)² + (y - 6)² = 11,5625

Bonjour,

Illustration graphique :