Soit un triangle ABC tel que AB= 9C cm AC= x cm et BC= x + 4 cm. Déterminer x pour que le triangle ABC soit un triangle rectangle.

[ReRe._12.]

Soit un triangle ABC tel que AB= 9C cm AC= x cm et BC= x + 4 cm. Déterminer x pour que le triangle ABC soit un triangle rectangle.

Merci de bien vouloir m'aider

[mtschoon]

@ReRe-_12 , bonjour,

Ici, la politesse n'est pas une option.
Ne pa l'oublier la prochaine fois.

Visiblement, ton schéma n'a pas passé.

Il faut utiliser le théorème de Pythagore, mais il faut que tu indiques le sommet de l'angle droit et la valeur de l'hypoténuse.

En plus, la valeur de AB est bizarre. On croit voir un C
AB=9 cm ou AB=90 cm ?

[mtschoon]

@ReRe-_12 ,A tout hasard :

Piste ,

Si le triangle est rectangle en A, si AB=9, si AC=x, et si BC=x+4 :

$B{C}^2=A{B}^2+A{C}^2$

$(x+4{)}^2=81+x^2$

Tu développes $(x+4{)}^2$ avec l'identité remarquable $(a+b{)}^2=a^2+b^2+2ab$

Ainsi, tu pourras s'implifier l'équation par $x^2$

Tu auras une équation du premier degré simple, pour trouver $x$

Remarque : si $AB=90$ alors $A{B}^2=8100$ et il faudra modifier

Reposte si besoin.

[mtschoon]

@ReRe-_12 ,

Représentation graphique ( si ma proposition est la bonne ...)

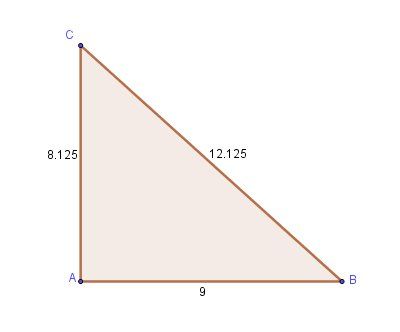
Et tu peux vérifier que :
$9^2+8,125^2=12.125^2$

[Black-Jack]

Bonjouir,

Si l'énoncé est bien tel qu'écrit (en précisant la vraie grandeur de AB) ...

Il y a 2 possibilités pour faire un triangle rectangle, la première est avec BC comme hypoténuse, la seconde avec AB comme hypoténuse.

Avec AB = 9 cm

1°) (x+4)² = x² + 9² (avec x > 0)
x = ...

2°) 9² = x² + (x + 4)² (avec x > 0)
x = ...

[mtschoon]

Bonsoir,

Comme @ReRe-_12 poste en Seconde , les équations du second degré ne s'étudient pas à ce niveau (elles s'étudient en Première) et passer par la forme canonique ne se fait pas en tout début d'année...

Alors, il y a de fortes chances (pour ne pas dire toutes) que l'exercice se ramène à résoudre une équation du premier degré.

C'est pour cela que "résoudre $(x+4{)}^2=x^2+9^2$" a été proposé et pas la possibilité se ramenant au second degré .

[Black-Jack]

Bonjour,

Si c'est le cas, alors l'énoncé, tel que rédigé, est bancal.

Tel que rédigé, Il y a 2 solutions, si on veut en exclure une, l'énoncé DOIT le faire en précisant soit la position de l'angle droit, soit en précisant quel est le coté hypoténuse.

Si on espère que les élèves acquièrent de la rigueur, il faut commencer par donner des énoncés rigoureux aussi.

[mtschoon]

Bonjour,

C'est sûr qu'avec un énoncé correct, il n'y aurait pas de problème!

@ReRe-_12 a obtenu : 
Cel prouve qu'il a voulu mettre un schéma mais qu'il n'y est pas arrivé.

Avec le schéma, tout aurait été clair et aurait levé tous les doutes sur l'énoncé.

[Clactar]

Ce message a été supprimé !