exercice prépa mathématiques

bonjour, j'ai un exercice sur lequel j'ai un peu de mal, le voici: $a l p h a$ désigne un réel quelconque. On considère la fonction f $a l p h a$ :x->((/x/^ $a l p h a$ )+1)/4x^2.

Déterminer le domaine de définition de f $a l p h a$ et étudier la parité de f $a l p h a$
On se concentre désormais sur l'étude de f $a l h p a$ sur R+étoile. Justifier que f $a l p h a$ est dérivable sur R+étoile et calculer f' $a l p h a$ (x) pour x>0.

SI vous pouviez m'aider sur ces deux points la ce serait déjà super. Voici ce que j'ai déjà fait:

x appartient Df pour tout x différent de 0 donc Df = (-infini;0)U(0;+infini). Les zeros sont bien sur exclus. En revanche pour étudier la parité je ne sais pas comment faire comme il y a la valeur absolue...
Pour cette question je ne sais pas comment on fait pour justifier cela hormis dire qu'elle est continue mais je ne pense pas que ce soit la rep attendue...
Merci par avance

Bonjour,

Parité

f(x) = ((|x|^alpha)+1)/(4x^2)

f(-x) = ((|-x|^alpha)+1)/(4*(-x)^2)
f(-x) = ((|x|^alpha)+1)/(4*x^2)

f(x) = f(-x) (pour tout x de Df) et donc f est paire.

Le graphe de f(x) est donc symétrique par rapport à l'axe des ordonnées.

On peut donc se limiter à étudier f sur R+* et à la fin déduire ce qui se passe sur R-* par symétrie du graphe par rapport à l'axe des ordonnées.

Sur R+*, on a |x| = x

et donc sur R*+, on a : f(x) = ((x^alpha)+1)/(4*x^2)

f'(x) = ...

mais en quoi dire que pour x>0 /x/ = x justifie que la fonction est dérivable sur R+étoile ?
En tout cas merci beaucoup. Pour la dérivée je trouve
f'(x)= ( $a l p h a$ x^ $a l p h a$ -1 x 4x^2 +8x^2 $a l p h a$ + 8x)/(4x^2)^2. C'est ca ?

@gregory Bonsoir,

Pour la dérivabilité, utilise les propriétés du cours, pour une fonction polynôme et une fonction rationnelle.

Pour la dérivée : $\dfrac{\alpha x^{\alpha-1}\times 4x^2-(x^{\alpha}+1)\times 8x}{16x^4}$
A simplifier.

d'accord merci.
Je trouve f'(x) = (16x^(2alpha-2) + 8x^(2alpha) + 8x)/16x^4. Est-ce juste ?

@gregory

Non,

$\dfrac{\alpha x^{\alpha-1}\times 4x^2-(x^{\alpha}+1)\times 8x}{16x^4}$

$\dfrac{\alpha x^{\alpha-1}\times x-(x^{\alpha}+1)\times 2}{4x^3}$

$\dfrac{\alpha x^{\alpha}-2x^{\alpha}-2}{4x^3}$

ah oui j'avais mis un + à la place du - parce que j'allais faire u x v au début en oubliant que c'était une fraction et j'ai oublié de le corriger quand j'ai corrigé le reste...
je dois maintenant résoudre f'>0.
J'ai dit que comme on est sur R+étoile le dénominateur est toujours >0 donc on cherche à résoudre $a l p h a$ x^ $a l p h a$ -2x^ $a l p h a$ - 2>0.
Je suppose que qu'il faut faire différents cas selon $a l p h a$ mais, faute de covid, j'ai jamais vus cela... Pourriez-vous m'expliquer brièvement ?
Merci beaucoup ️

Bonjour,

@gregory , pistes pour poursuivre,

Si j'ai bien lu, pour x>0, tu veux résoudre $αxα−2xα−2>0\alpha x^\alpha-2x^\alpha-2\gt 0$

Commence par factoriser :
$(α−2)xα−2>0(\alpha-2)x^\alpha-2\gt 0$

Transpose 2 :
$(α−2)xα>2(\alpha-2)x^\alpha\gt 2$

Pour diviser par $(α−2)(\alpha -2)$ , tu dois discuter suivant son signe.

Fais 3 cas :

1er cas : $α=2\alpha=2$ c'est à dire $α−2=0\alpha-2=0$ d'où...

2ème cas : $α>2\alpha\gt2$ c'est à dire $α−2>0\alpha-2\gt 0$
Tu divises sans changer le sens de l'inéquation, d'où...

3ème cas : $α<2\alpha\lt 2$ c'est à dire $α−2<0\alpha-2\lt 0$
Tu divises en changeant le sens de l'inéquation, d'où...

Bonjour, merci !

1er cas: $a l p h a$ =2 <=> 0>2 impossible donc $a l p h a$ ne peut pas être égale à 2.
2eme cas: alpha>2 <=> $a l p h a$ -2>0 d'ou ( $a l p h a$ -2)x^ $a l p h a$ >2 car exponentielle est toujours >0 donc $alpha peut être supérieur à 2
3eme cas: $a l p h a$ <2 <=> $a l p h a$ -2<0 donc $a l p h a$ <2 d'ou ( $a l p h a$ -2)x^ $a l p h a$ <2 donc alpha peut pas être inférieur à 2 .
Ainsi on a $a l p h a$ appartient à (2exclu;+infini) pour résoudre cette inéquation c'est ça ?
Merci pour le temps que vous m'accorder.

@gregory , si le but est de résoudre, pour $x>0x\gt 0$ l'inéquation :
$(α−2)xα>2(\alpha-2)x^\alpha\gt 2$ , tu n'as pas terminé.

Effectivement , c'est le 2ème cas qui convient mais, pour $α>2\alpha\gt 2$ , il faut déterminer x solution de l'inéquation.

$xα>2α−2x^\alpha \gt \dfrac{2}{\alpha-2}$ donc $x$ .....................

euh je ne vois pas...

@gregory ,
Si tu connais, tu peux écrire directement
$x>(2α−2)1αx\gt \biggr(\dfrac{2}{\alpha-2}\biggr)^{\dfrac{1}{\alpha}}$

Sinon, tu peux passer par le logarithme népérien , mais c'est beaucoup plus long...

$xα>2α−2x^\alpha\gt \dfrac{2}{\alpha-2}$

$ln(xα)>ln(2α−2)ln(x^\alpha)\gt ln(\dfrac{2}{\alpha-2})$

$αlnx>ln(2α−2)\alpha lnx\gt ln(\dfrac{2}{\alpha-2})$

$lnx>1αln(2α−2)lnx\gt\dfrac{1}{\alpha} ln(\dfrac{2}{\alpha-2})$

$x>e1αln(2α−2)x\gt e^{\dfrac{1}{\alpha} ln(\dfrac{2}{\alpha-2})}$

$x>(eln(2α−2))1αx\gt \biggr(e^{ln(\dfrac{2}{\alpha-2})}\biggr)^{\dfrac{1}{\alpha}}$

$x>(2α−2)1αx\gt (\dfrac{2}{\alpha-2})^{\dfrac{1}{\alpha}}$

d'accord merci, je vais passer par le logarithme c'est mieux.
Donc ma conclusion précédente est bonne ? Je dois juste rajouter cela pour $a l p h a$ >2 ?

@gregory ,

Oui ce calcul est valable dans le cas $α>2\alpha\gt 2$ (deuxième cas de la discussion)

Les deux autres cas étaient bons.

d'accord merci, il me reste un dernier point à éclaircir.
Je dois montrer que si alpha>2 la fonction admet un minimum sur (O exclu; +infini). Comment faire ?

@gregory , ta dernière question est la conséquence de ce qui vient d'être fait , pour $α>2\alpha \gt 2$

$f′(x)>0f'(x)\gt 0$ <=> $x>(2α−2)1αx\gt \biggr(\dfrac{2}{\alpha-2}\biggr)^\dfrac{1}{\alpha}$
Avec la même démarche, tu dois trouver :
$f^{'} (x) = 0$ <=> $\biggr(\dfrac{2}{\alpha-2}\biggr)^\dfrac{1}{\alpha}$
$f′(x)<0f'(x)\lt 0$ <=> $x<(2α−2)1αx\lt \biggr(\dfrac{2}{\alpha-2}\biggr)^\dfrac{1}{\alpha}$

Donc le minimum est pour $x = . . . . . . . . . . .$

Fais éventuellement le tableau de variation pour plus de clarté

@gregory , bonjour,

J'espère que tu as trouvé que le minimum est pour
$x=(22−α)1αx=\biggr(\dfrac{2}{2-\alpha}\biggr)^\dfrac{1}{\alpha}$

Revois tout ça de près.
Bon travail.

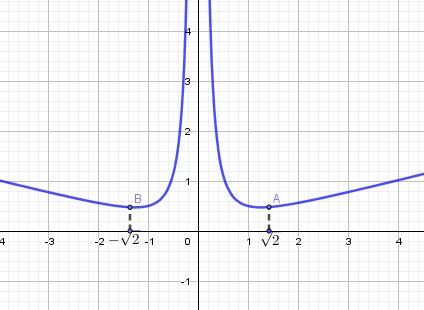
Illustration graphique pour $α>2\alpha\gt 2$ ,

$α=3\alpha=3$

$f3(x)=∣x∣3+14x2f_3(x)=\dfrac{|x|^3+1}{4x^2}$

$(2α−2)1α=2\biggr(\dfrac{2}{\alpha-2}\biggr)^\dfrac{1}{\alpha}=\sqrt 2$

ce que j'ai du mal a comprendre dans cette exercice c'est ce que je dois faire du alpha et les différentes démarches pour parvenir au résultat attendu, par exemple pour trouver la dernière question que je vous ai posé; je comprends tout à fait que f'(x)<0 <=> x<(2/alpha-2)^1/alpha mais après que dois-je faire ? Je ne comprends pas bien comment résoudre cela le alpha me brouille...
En tout cas merci encore pour votre aide !

@gregory ,

$α\alpha$ est le paramètre ( parfois on dit qu'un paramètre est une "constante qui varie"...!). C'est imagé, mais ça permet de comprendre (peut-être)

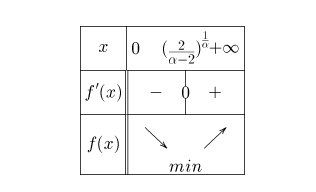
Comme déjà indiqué, pour la dernière question, pour $α>2\alpha \gt 2$ , fais le tableau de variation de f sur $]0,+∞[]0,+\infty[$ :
Une ligne pour $x$ avec, entre 0 et $+∞+\infty$ , la valeur $(2α−2)1α\biggr(\dfrac{2}{\alpha-2}\biggr)^\dfrac{1}{\alpha}$
Une ligne pour $f^{'} (x)$ avec les signes (de gauche à droite) - 0 +
Une ligne pour f avec flèche descendante puis montante.

Tu devrais ainsi réaliser le minimum.

Ici, $α\alpha$ est une constante qui peut prendre n'importe quelle valeur strictement supérieure à 2
Dans le schéma que je t'ai indiqué dans ma précédente réponse, j'ai pris $α=3\alpha=3$

@gregory , si c'est le paramètre $α\alpha$ qui te bloque, je te conseille de regarder des exercices corrigés de Première/Terminale où interviennent un paramètre.

Ici, par exemple, il s'agit d'une équation du second degré avec un paramètre qui s'appelle m (au lieu de $α\alpha$ dans ton exercice).

https://www.youtube.com/watch?v=m0544Av_XFA

Bonne lecture.

D’accord j’ai tout fini et j’ai repris j’ai réussi à le refaire. Merci pour tout !

De rien @gregory ,

C'est parfait si tu as pu tout refaire seul !

Bon travail !