Dérivée des fonctions ln
-
Eemilio49 dernière édition par
Bonsoir moi c’est Emilio je suis un peu bloqué sur un exercice de ln. on me demande de donner la dérive de f(x)=1/2[lnx-ln(1-x)]
Merci d’avance pour votre aide.
-
mtschoon dernière édition par mtschoon

@emilio49 , bonsoir,
Ladérivée de ln(x)ln(x)ln(x) est 1x\dfrac{1}{x}x1
UUU étant une fonction de xxx, la dérivée de ln(U(x))ln(U(x))ln(U(x)) est U′(x)U(x)\dfrac{U'(x)}{U(x)}U(x)U′(x)
Si j'ai bien lu,
f(x)=12(lnx−ln(1−x))f(x)=\dfrac{1}{2}(lnx-ln(1-x))f(x)=21(lnx−ln(1−x))Tu dois donc trouver :
f′(x)=12(1x+11−x)f'(x)=\dfrac{1}{2}\biggr(\dfrac{1}{x}+\dfrac{1}{1-x}\biggr)f′(x)=21(x1+1−x1)Bon calcul.
-
mtschoon dernière édition par mtschoon

@emilio49 , bonjour,
Evidemment, si le but de l'exercice est d'étudier les variations de f, tu peux conclure.
Tout d'abord, tu as, je suppose, donné l'ensemble de définition (qui ici aussi le domaine de de dérivabilité)
Conditions : x>0x\gt 0x>0 et 1−x>01-x\gt 01−x>0
1−x>01-x\gt 01−x>0 <=>−x>−1-x \gt -1−x>−1 <=> x<1x\lt 1x<1
Au final , Df=Df′=]0,1[Df=Df'=]0,1[Df=Df′=]0,1[
Pour tout xxx de ]0,1[]0,1[]0,1[, f′(x)>0f'(x)\gt 0f′(x)>0 donc f strictement croissante.
-
mtschoon dernière édition par

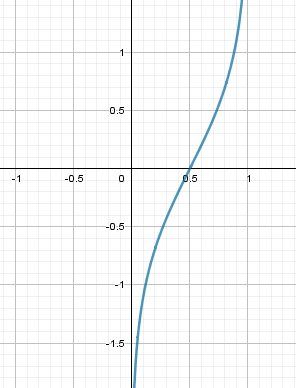
Illustration graphique
Les droites d'équation x=0x=0x=0 et x=1x=1x=1 sont asymptotes à la courbe.