suite d'evennement et probabilite totale

bonsoir a tous !

Un fumeur décide d' arrêter. On suppose que si cette personne n'a pas fumé le jour n, alors la probabilité qu'elle
fume le jour suivant est égale à 0,1. Mais si cette personne fume le jour n, sa probabilité de fumer le jour suivant est égale à 0,8.
1 . Exprimer la probabilité que cette personne fume le
jour n + l en fonction de la probabilité qu'elle fume
le jour n.
2. Déterminer la limite de cette probabilité avec n. Estce que cette personne va s' arrêter de fumer ?

je bloque un peu sur cet exercice
pour la question 1 je fais $\cap n+1) = P(n) * P(n+1/ n)$ or $P (n + 1 / n) = P (n + 1)$ d'ou
$\frac{P(n \cap n+1)}{P(n)}$ avec $P (n + 1) = 0.8$
cette forme ne me permet pas ce calculer la limite pour la question 2
merci de m'eclaicir

@loicstephan Bonjour,

Fais un arbre pondéré.
Il manque un terme à ton calcul.
$P(Fn+1)=P(Fn+1/Fn)×P(Fn)+P(Fn+1/F(n)‾)×P(Fn‾)P(F_{n+1})=P(F_{n+1}/F_{n})\times P(F_n)+P({F_{n+1}}/\overline{F(n)})\times P(\overline{Fn})$

Bonjour,

Oui, un arbre pondéré est très utile .
J'en joins un.

Notations (même si certaines ne servent pas):
$F_n$ évènement "fumer le jour n"
$Fn‾:\overline{F_n} :$ évènement "ne pas fumer le jour n"
$F_{n+1}$ : évènement "fumer le jour n+1"
$Fn+1‾\overline{F_{n+1}}$ évènement "ne pas fumer le jour n+1"
$p_n$ probabilité de fumer le jour n
$1-p_n$ probabilité de ne pas fumer le jour n
$p_{n+1}$ probabilité de fumer le jour n+1
$1-p_{n+1}$ probabilité de ne pas fumer le jour n+1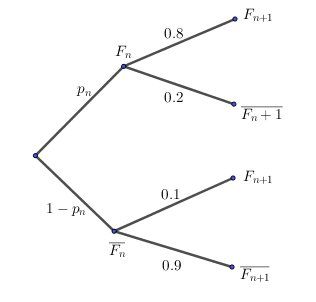

L'arbre clarifie bien la situation.

D'où :
$p_{n+1}=(p_n)(0.8)+(1-p_n)(0.1)$

j'ai fait l'arbre mais j'ai perdu de vue que $F_{n+1}$ dependait egalement de la proabilité de n'avoir pas fumer le jour n soit je ne prennais pas en compte la branche du bas! bon je fais l question 2 et je vous fait part des resultats

sauf erreur de ma part la limte en n $P_{n+1}$ en n lorsque n tend vers l'infinie est une limite infinie la conclusion est que plus les jours passe plus l probabilite de fumer tend vers l'infini conclusion la personne ne pourra arreter de fumer

@loicstephan

A partir de la relation :
$pn+1=pn×0,8+(1−pn)×0,1p_{n+1}=p_n\times0,8+(1-p_n)\times 0,1$
soit
$pn+1=pn×0,7+0,1p_{n+1}=p_n\times0,7+ 0,1$

Pour calculer la limite $l$ , tu résous l'équation :
$l = 0, 7 l + 0, 1$

Je te laisse poursuivre.

DEJA je trouve la solution $13\frac{1}{3}$ soit une limite finie quelle est donc la conclusion d'abord mais aussi pourquoi doit on poser $P_{n+1}=P_n=l$ pour trouver la limite

@loicstephan

C'est une limite donc on considère que $P_{n+1}=P_n = l$
Pour la conclusion, à quoi correspond $P_{n+1}$ ?

la probabilite de fumer les jours futurs dans e cas il pouras s'arreter de fumer etant donné que sa probabilité de fumer pour les jours a venir est une limite finie

Bonjour,

@loicstephan , pour ta seconde question, il s'agit du "théorème du point fixe" qui conclut que la limite de la suite $p_n)$ vérifie $l = 0.7 l + 0.1$
Il devrait être dans ton cours.(en principe...)

Pour comprendre intuitivement ce théorème :
Tu peux penser que si la suite $p_n)$ est convergente vers une valeur finie $l$ , lorque n tend vers + $∞\infty$ , $p_n$ et $p_{n+1}$ tendent vers $l$
Donc, par passage à la limite, l'égalité $p_{n+1}=0.7p_n+0.1$ devient : $l = 0.7 l + 0.1$

J'ignore le niveau de rigueur exigé...mais, en toute rigeur, pour appliquer ce théorème, il faudrait prouver d'abord que cette suite $p_n)$ est convergente vers une limite finie $l$ , ce qui n'est pas fait.

Tu peux contourner cet obstacle.
Tu sais que $p_{n+1}=0.7p_n+0.1$

Tu résous l'équation $x = 0.7 x + 0.1$ tu trouves $13\dfrac{1}{3}$
Soit $l$ cette valeur $13\dfrac{1}{3}$

Tu as donc :
$p_{n+1}=0.7p_n+0.1$
$l = 0.7 l + 0.1$

En retanchant membre à membre :
$p_{n+1}-l=0.7(p_n-l)$

Tu poses : $U_n=p_n-l$ d'où : $U_{n+1}=p_{n+1}-l$
donc $U_{n+1}=0.7U_n$

$U_n)$ est une suite géométrique de raison $0.7$
$0.7$ est compris entre 0 et 1 donc la suite $U_n)$ converge vers 0
d'où:
$lim⁡n→+∞Un=0\displaystyle \lim_{n\to +\infty}U_n=0$
$lim⁡n→+∞(pn−l)=0\displaystyle \lim_{n\to +\infty}(p_n-l)=0$
$lim⁡n→+∞pn=l\displaystyle \lim_{n\to +\infty}p_n=l$

La suite $p_n)$ a donc pour limite $l=13l=\dfrac{1}{3}$

Cette personne ne va donc pas s' arrêter de fumer...dommage pour elle...

Bon travail.

@mtschoon
merci beaucoup pour les details merci !!!

De rien @loicstephan ,

J'espère que c'est clair pour toi.

@mtschoon a dit dans suite d'evennement et probabilite totale :

En retanchant membre à membre :
pn+1−l=0.7(pn−l)p_{n+1}-l=0.7(p_n-l)pn+1−l=0.7(pn−l)
Tu poses : Un=pn−lU_n=p_n-lUn=pn−l d'où : Un+1=pn+1−lU_{n+1}=p_{n+1}-lUn+1=pn+1−l
donc Un+1=0.7UnU_{n+1}=0.7U_nUn+1=0.7Un

bonjour!
en regardant cette demontration je me demande ou est passé $0.1$