DM maths exo 2 FONCTION POLYNOME

[yaya1810]

AEDC est un rectangle tel que AC = 7 et AE = 2, comme représenté ci-contre.B est un point de [AC] tel que AB = 5.P est un point de [ED] tel que EP = x.On note f(x) = PA2 + PB2 + PC2. Démontrer que f admet un minimum, puis déterminer la valeur de ce minimum ainsi que la valeur de x pour laquelle il est atteint.

[mtschoon]

@Cécilia-Bourgeois , re-bonjour.

Tu as une figure (d'après ce que tu écris)

Tu peux la joindre.
(Ici, les scans d'énoncés ne sont pas autorisés mais les scans de graphiques sont autorisés)

Je pense qu'il faut comprendre :
$f(x)=P{A}^2+P{B}^2+P{C}^2$

[mtschoon]

@Cécilia-Bourgeois ,

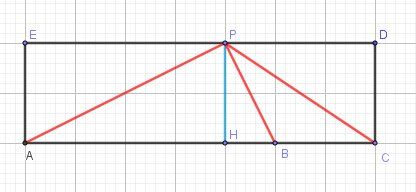
Je joins une image, à adapter si car j'ignore la disposition du schéma de ton énoncé.
,

[mtschoon]

@Cécilia-Bourgeois ,

Pistes,
Soit H le projeté orthogonal de P sur (AC)

Pour $0\le x\le 7$
$AH=x$
$HB=AB-AH=5-x$
$HC=AC-AH=7-x$

Tu utilises 3 fois le Théorème de Pythagore .

Dans le triangle rectangle PAH :
$P{A}^2=A{H}^2+H{P}^2=x^2+2^2=x^2+4$

Pour exprimer $P{B}^2$, tu utilises le triangle rectangle PBH
Pour exprimer $P{C}^2$, tu utilises le triangle rectangle PCH

En ajoutant ces 3 expressions, en développant les identités remarquables et en simplifiant, tu dois trouver un polynôme du second degré $3x^2-24x+86$ (à vérifier)

Pour trouver le minimum, tu utilises la méthode vue dans ton topic précédent.

Reposte si besoin , ou pour indiquer tes réponses pour vérification.

[yaya1810]

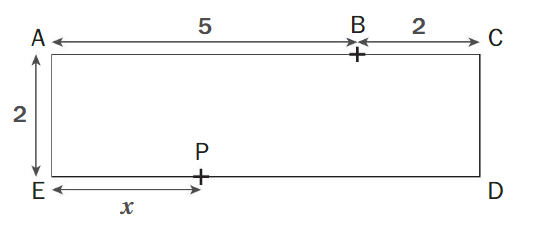
VOICI LA FIGURE

[mtschoon]

@Cécilia-Bourgeois , merci pour la figure.

Il faut donc que tu la complètes en plaçant H projeté orthogonal de P sur (AC) et que tu traces les segments [PH], [PA], [PB], [PC]

[yaya1810]

Je ne comprends pas j'obtiens PB^2=PH^2+HB^2= 2^2+5-x= 9-x
et PC^2= PH^2+HB^2=2^2+7-x=11-x
et du coup je fais : x^2+4+9-x+11-x et donc je n'obtient pas le résultat que vous dites

[mtschoon]

@Cécilia-Bourgeois , je regarde.

Je pense que tu as oublié les carrés.

$P{B}^2=P{H}^2+H{B}^2=2^2+(5-x{)}^2$
$P{B}^2=4+25-10x+x^2=29-10x+x^2$

De même,
$P{C}^2=P{H}^2+H{B}^2=2^2+(7-x{)}^2$
A développer et simplifier.

J'ai vérifé le total.
Sauf erreur, ça devrait faire :
$f(x)=3x^2-24x+86$

Reposte si besoin.

[yaya1810]

@mtschoon
Bonjour,
C’est bon j’ai réussi mon calcul et j’ai mieux compris les deux exercices je vous remercie, et je suis reconnaissante en vers vous. Vous m’avez énormément aidé encore merci.
Bonne journée

[mtschoon]

De rien @Cécilia-Bourgeois ,

Très contente de t'avoir aidée.

Reviens quand tu as besoin.