approximation de la loi de poisson par loi binomiale

Bonjour,
Je ne comprends pas une notion dans cet exercice.
Le grand nombre d’aberrations chromosomiques est une marque significative du cancer. On dispose de 10 noyaux de cellules tumorales. Pour chaque noyau i, la variable aléatoire Xi compte le nombre d’aberrations chromosomiques. Pour tout i, L(Xi) = P(6) et les variables aléatoires Xi sont indépendantes. Soit X =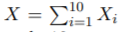 la variable aléatoire qui compte le nombre d’aberrations chromosomiques de l’échantillon de 10 noyaux de cellules tumorales.

Peut-on approcher la loi de X par une loi normale? Pourquoi ?

De la même manière, la variable aléatoire Y compte le nombre d’aberrations chromosomiques dans un échantillon de 10 noyaux de cellules saines (non tumorales). Pour chaque noyau, le nombre d’aberrations chromosomiques suit la loi P(0, 8).

Par quelle loi peut-on approcher cette loi ?
Quelle est la probabilité p qu’un noyau de cellule saine ne présente aucune aberration chromosomique ?

Ce qui me dérange dans la correction c'est qu'on utilise la loi binomiale et qu'on dit que la probabilité de n'obtenir aucune aberrations chromosomiques vaut p=e^(-0,8) ce que je ne comprends absolument pas

D'ailleurs je voudrais comprendre pourquoi on utilise pour l'approximation la loi binomiale.

deja pour approximer un phenomene par la loi normale if faudrait que le nombre d'observation soit $≥30\geq 30$ ainsi on dit que le phenomene est normal!

parce que pour chaque noyaus de cellule saine il y a deux possibilités soit presence d'une aberation chromosomique soit l'ansence!

@MOUNA8 , bonjour,

Je regarde tes questions.
Si j'ai bien lu, tu as la correction de l'exercice et tu as des doutes.
Pour pouvoir répondre à cela avec sérieux, il faudrait que tu donnes cette correction, ce qui n'est pas le cas.

Alors, je te donne seulement des indications générales sur cet exercice.

Dans certaines conditions, effectivement, la loi binomiale $B (n, p$ ) peut être remplacée par la loi de Poisson $P (n p)$ .
Les conditions usuelles sont $p≤0.1p\le 0.1$ , $n≥30n\ge 30$ et $np<15np\lt 15$ (certains indiquent plutôt $np≤10np\le 10$ )
Je te mets un lien :
https://www.youtube.com/watch?v=CFNlaMrwO4o

Bien sûr, pour pouvoir utiliser cette propriété de remplacement, il faut connaître n et p.

Pistes pour tes questions.

Première partie 1.
La réponse est Oui.

Si j'ai bien compris ce que tu veux dire par "L(Xi)=P(6)" , $X_i$ suit la loi de Poisson de paramètre $λ=6\lambda=6$

Tu dois connaître la propriété d'additivité de la loi de Poisson.
http://www.jybaudot.fr/Probas/addipoisson.html

Sur l'échantillon des 10 noyaux, X suit la loi de Poisson de paramètre $λ=6+6+...+6=10×6=60\lambda=6+6+...+6=10\times 6=60$

Lorsque le paramètre λ est grand (en pratique supérieur à 25), une loi de Poisson peut être approchée par une loi normale d'espérance λ et de variance λ.

Ici, $λ=60\lambda=60$ donc c'est bon.

@MOUNA8 ,
Ce que je dirais seulement sur la seconde partie...

Seconde partie 1.
$λ=0.8×10=8\lambda=0.8\times 10=8$
La loi Y, avec le même principe qu'à la question précédente, suit la loi de Poisson $(P, 8)$

Seconde partie 2.
Il s'agit maintenant seulement d'un seul noyau. Je note $Y_i$ la variable de loi $(P, 0.8)$

Tu sais que :
$Pr(Yi=k)=e−λλkk!Pr(Y_i=k)=\dfrac{e^{-\lambda}\lambda^k }{k!}$

Donc : $p=Pr(Yi=0)=e−λλ00!p=Pr(Y_i=0)=\dfrac{e^{-\lambda}\lambda^0 }{0!}$

Ce qui donne : $p=Pr(Yi=0)=e−λ=e−0.8p=Pr(Y_i=0)=e^{-\lambda}=\boxed{e^{-0.8}}$

Comme déjà indiqué, il faudrait pouvoir consulter la correction pour donner un avis dessus...