exercice probabilité

[phenix]

Ce message a été supprimé !

[mtschoon]

Début de l'énoncé, reconstutué de mémoire, vu que @phenix l'a effacé après avoir obtenu de l'aide !....

Enoncé :
Un quart de la population d'une région a été vacciné contre la grippe.
Sur 10 malades, un seul a été vacciné
sur 15 personnes vaccinées, une seule est malade.
On se sert de ces statistiques pour faire des calculs de probabilités.
Soit M : la personne est malade
Soit V : la personne est vaccinée

1. Construire un arbre pondéré pour calculer $P(M)$
2. Donner $P_V(M)$
3. Compléter entièrement l'arbre.

Il y avait ensuite des questions (utilisant la loi binomiale) sur des joueurs de foot, handball, rygby, puis n personnes , mais ces questions n'ayant pas étaient traitées, je ne me souviens pas de l'énoncé exact.

Réponse :
@phenix , bonjour,
Je te mets quelques pistes pour démarrer,
Tu fais d'abord l'arbre avec les données de l'énoncé et tu l'utilises pour faire les calculs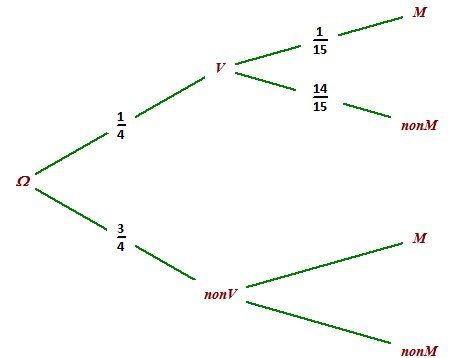

Sur l'arbre
$\overline{V}$ est noté nonV
$\overline{V}$ est noté nonM

$P(V\cap M)=\frac{1}{4}\times \frac{1}{15}=\frac{1}{60}$

$P(V\cap M)$ peut aussi s'écrire $P(M)\times p_M(V)$

Donc : $\frac{1}{60}=P(M)\times \frac{1}{10}$

Tu peux déduire que $P(M)=\frac{1}{6}$

Je te laisse poursuivre.

[mtschoon]

@phenix , ici , il y a un exercice de Bac, qui n'est pas le même que le tien mais qui est dans le même esprit.
https://www.freemaths.fr/corriges-par-theme/bac-s-mathematiques-france-metropolitaine-2018-obligatoire-corrige-exercice-2-probabilites-discretes.pdf

Tu peux le consulter et le travailler .
ça devrait t'aider.

[phenix]

@mtschoon merci beaucoup pour l'aide

[Black-Jack]

Merde alors,

Encore un quidam qui supprime son message une fois l'aide obtenue.

C'est peut-être permis ... mais cela reste inacceptable et mesquin.

[mtschoon]

@Black-Jack a dit dans exercice probabilité :

Encore un quidam qui supprime son message une fois l'aide obtenue.

C'est peut-être permis ... mais cela reste inacceptable et mesquin.

Je suis totalement d'accord avec cette analyse .

Comme j'ai répondu à ce topic, de mémoire, je vais reconstituer la partie de l'énoncé correspondant à mon aide (au début de ma réponse) pour que ceux qui viennent consulter puissent comprendre.
C'est le but d'un forum public, il me semble : que tous ceux qui le veulent , puissent travailler et progresser.