Maths complémentaire suites numérique

Bonjour ,
Je voudrais de l'aide pour mon exercice suivant car je me suis perdue dans les calculs

Un club de sport compte en 2020, 300 menbres. Chaque année 90% des membres renouvellent leur adhésion et on compte 50 nouveaux membres.

Modéliser cette situation par une suite (un)
A laide d'un graphique déterminer les premiers termes de la suite
Conjecturer le sens de variation de u(n) et sa limite
Déterminer une suite constante vérifiant la même relation de reccurence que la suite u(n)
5 . En déduire l'expression de u(n) en fonction de n
En déduire la limite de la suite u(n) interpréter

Pour la 1 j'ai trouvé u(n)= 0,9 ^ n +50
Et u n+1= 300*0,9^n+50
Je ne suis pas sûre
Pour la deux , il faut graduer a combien 10 par 10?
Par un?
Par 50 je suis perdue
Merci d'avance

@maybessa , bonjour,
J'ai mélangé tes deux topics !
C'était sur l'autre que tu parlais de Python.
Je n'ai pas l'habitude du langage Python , mais je peux de dire que Tant que se traduit par while

Tu peux éventuellemnt consulter ici :
https://info.sio2.be/python/3/2.php

@mtschoon
D'accord merci quand même

@maybessa merciii

@mtschoon
Et pour cet exercice ci le suite est celle ci ou c'est faux?

@maybessa , oui, tu as mal commencé.

Je regarde ta question.

Ta réponse à la 1) est bizarre...

C'est plutôt $U_{n+1}=0.9U_n+50$

@mtschoon
Oh j'ai inversé donc u(n) est égale à quoi... U(0) = 300?
Donc sur le graphique on gradué de 50 en 50?
U(n) = 300*0,9^n + 50?

@maybessa
J'ai fait le graphique,
En graduant de 50 en 50
U(0) vaut 300
U(1) vaut environ 320
U(2) vaut 330
U(3) vaut environ 345 je dois le faire au propre pour être sûr des valeurs

Le suite u n est donc sa limite tend vers 400?
Je n'ai pas compris la 4

@maybessa ,

S j'ai bien lu, $U_0=300$

$U_{n+1}=0.9U_n+50$

Tu dois déterminer les valeurs de $U_n$ de proche en proche avec un graphique.

Je te calcules $U_1$ et $U_2$ ( pour comprendre ) mais l'énoncé de dit de les déterminer graphiquement.

$U1=0.9U0+50=0.9×300+50=320U_1=0.9U_0+50=0.9\times 300+50=320$
$U2=0.9U1+50=0.9×320+50=338U_2=0.9U_1+50=0.9\times 320+50=338$

Je t'indique le début la liste de ce que tu devrais trouver si tu devais faire les calculs pour te faire une idée :

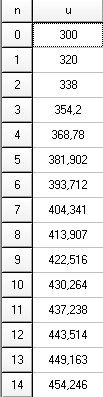
Tu dois observer que la suite est croissante et que la limite est 500

@mtschoon
J'ai mal lu sur mon graphique avec la limite
La suite constante est donc 50/ 1- 0,9 donc 500?

@maybessa ,

Piste pour la 4)

Soit K la valeur unique de la suite constante vérifiant la même relation de reccurence que la suite $U_n)$

Vu que $U_{n+1}=0.9U_n+50$

La valeur de K vérifie : $K = 0.9 K + 50$

Tu résous cette équation pour trouver la valeur de K.

@maybessa

Nos messages se sont coisés...

Ta dernière réponse (500) est exacte.

@mtschoon
Oui j'ai vu je suis perdue pour la 5

@maybessa ,

Pour la 5), tu peux poser $V_n=U_n-500$

Tu démontres que $V_n)$ est une suite géométrique .

Tu trouves l'expression de $V_n$ puis de $U_n$

@mtschoon
Mercii je vais suivre cette piste pour trouver la réponse merci

@mtschoon
J'ai trouvé en détaillant que v (n+1). = O,9vn
Donc de raison 0,9 et de premier terme v(0)= -200
Car v(0)= u(0)-500

Un= v(0)+500
U(n) = 0,9^n * -200 +500

Lim 0,9 = 0
Lim u(n) vaut donc 500?

@maybessa
Donc pour interpréter le club de sport ne dépassera jamais les 500 membres dans les années qui suivent?

@maybessa ,

Tu as fait quelques fautes de frappe .

Je pense que tu as voulu écire :

$lim⁡n→+∞(0.9)n=0\displaystyle \lim_{n\to +\infty}(0.9)^n=0$

$U_n=V_n+500$

A par ça, tout est bon.

La limite de $U_n)$ est bien 500, vu que la limite de $V_n)$ est 0 .

@mtschoon
Oui désolé mercii beaucoup pour votre aide

De rien @maybessa .

Bon travail et bonne fin de week-end.

PS : Effectivement, le club de sport ne dépassera jamais les 500 membres dans les années qui suivent.