Salut tous le monde, s ils vous plait j ve calculer cette integrale, jai deja essaye l integration par parties mais avec aucun resultat.

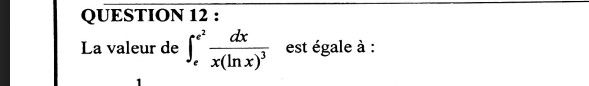
@Imad-Hafidi Bonjour,

L'expression est de la forme $U′U3\dfrac{U'}{U^3}$ donc une primitive est $−12U2-\dfrac{1}{2U^2}$

avec $U = l n x$ .

Je te laisse poursuivre le calcul.

Bonjour,

On l'a vu il y a peu de temps cette intégrale.

J'explicite un peu si besoin (vu que tu postes en Sup, @Imad-Hafidi , tu a dû voir d'autres méthodes)

Par exemple :

$U = l n x$ donc $U′=1xU'=\dfrac{1}{x}$

$1x(lnx)3=(lnx)−3)×1x=U−3U′\dfrac{1}{x(lnx)^3}=(lnx)^{-3})\times \dfrac{1}{x}=U^{-3}U'$

Une primitive $U−3+1−3+1=U−2−2=−12U2=−12(lnx)2\dfrac{U^{-3+1}}{-3+1}=\dfrac{U^{-2}}{-2}=-\dfrac{1}{2U^2}=\dfrac{-1}{2(lnx)^2}$

Soit I l'intégrale cherchée.

$I=[−12(lnx)2]ee2=−12(lne2)2+12(lne)2I=\biggr[\dfrac{-1}{2(lnx)^2}\biggr]_e^{e^2}=\dfrac{-1}{2(lne^2)^2}+\dfrac{1}{2(lne)^2}$

Après transformation des ln, tu dois trouver, sauf erreur, $I=38I=\dfrac{3}{8}$

@Noemi Merciii enormement.

@mtschoon Merci a vous.