Devoir de mathématiques sur triangle et rectangle
-
Patrick De France dernière édition par Noemi
Bonjouur, j'ai un dm à rendre et je suis bloqué, je ne comprends rien du tout...
Est ce que quelqu'un pourrait me donner les réponses des premières questions pour me mettre sur la piste, merci
CordialementScan supprimé par la modération.
-
@Patrick-De-France Bonjour,
Le scan de l'énoncé de l'exercice est interdit sur ce forum.
Seuls les scans de schémas, graphiques ou figures sont autorisés.Laisse la figure représentant le triangle mais écris l'énoncé.
Le scan va être supprimé.
-
Patrick De France dernière édition par Noemi
Désolé pour avoir pris un scan... Voici l'exercice complet
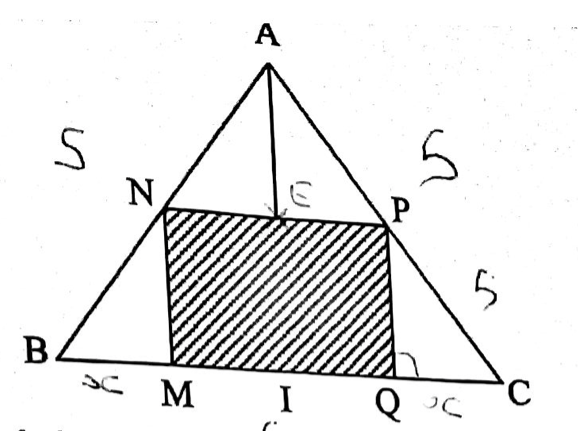
ABC est un triangle isocèle de sommet A tel que AB=AC = 5 et BC= 6. On désigne par I le milieu du segment [BC]. À tout point M du segment [BI], on associe le rectangle MNPQ comme le montre la figure ci-dessus. On pose BM=x.
On désigne par f(x) et g(x) les aires respectives du rectangle MNPQ et du triangle ANP.
- Quel est l'ensemble de définition des fonctions fet g? 2. Exprimer les longueurs MN et MQ en fonction de x.
Pour quelle valeur de x le rectangle MNPQ est-il un carré ?
- Montrer que:
4 4 f(x) = x(6−2x) et g(x) = x² − 8x +12. 3
- Tracer sur un même graphique les courbes représentatives de f et g. 5. À l'aide du graphique précédent, répondre aux questions suivantes : a) Construire le tableau de variation de f et g.
b) Pour quelle valeur de x l'aire du rectangle MNPQ est-elle maximale ? c) Pour quelles valeurs de x le rectangle MNPQ a-t-il une aire supérieure ou
égale au quart de celle du triangle ABC? d) Pour quelle(s) valeur(s) les aires du rectangle MNPQ et du triangle ANP
sont-elles égales ?
J'ai réussi à la 1 et la 2 mais je bloque a la 3, est ce que quelqu'un pourrait m'aider s'il vous plaît
MerciFigure mise en ligne par la modération.
-
mtschoon dernière édition par mtschoon

@Patrick-De-France, bonsoir,
Comme indiqué, il faut donner le graphique...
-
Question 3
Vérifie l'énoncé, notamment l'écriture des fonctions.
Calcule la mesure de la hauteur AI, puis celle de MN.
-
mtschoon dernière édition par

Bonsoir,
Merci @Patrick-De-France , pour le graphique.
Je trouve quelque chose de bizarre.
La formule f(x)=x(6−2x)f(x)=x(6-2x)f(x)=x(6−2x) est-elle donnée dans l'énoncé ?
MQ=BC−(BM+CQ)=6−2xMQ=BC-(BM+CQ)=6-2xMQ=BC−(BM+CQ)=6−2x
f(x)=aire(MNPQ)=MN×MQf(x)=aire(MNPQ)=MN\times MQf(x)=aire(MNPQ)=MN×MQ
Il faudrait donc MN=xMN=xMN=x, ce qui n'est pas possible...
En effet, tu dois trouver (Pythagore) AI=4AI=4AI=4
Thalès : MNAI=BMBI\dfrac{MN}{AI}=\dfrac{BM}{BI}AIMN=BIBM <=> MN4=x3\dfrac{MN}{4}=\dfrac{x}{3}4MN=3x
D'où MN=4x3MN=\dfrac{4x}{3}MN=34x
Contradiction...
Je reste perplexe.