Convergence d'une Somme de termes.

[Wil Fried]

Aidez moi svp.
Soit la suite ($U_n(\alpha )$) définie pour tout $\alpha >0$ : $U_n(\alpha )={\sum }_{k=1}^n\frac{1}{k^{\alpha }}$

1. Étudier la convergence de la suite ($U_n(\alpha )$)
2. Trouver un encadrement de la limite de ($U_n(\alpha$)) quand elle existe.
3. Interpréter géographiquement ($U_n(\alpha )$).

[mtschoon]

@Wil-Fried , bonsoir,

Je suis surprise de cet exercice en Terminale .
La suite dont tu parles est la "Série de Reimann"

Tu peux trouver des explications sur le web.
En principe, cela se fait en cours en Sup, et on te demande de le faire en exercice ...en Terminale . C'est très bizarre...

Je te mets quelques pistes,

$U_n(\alpha )=\frac{1}{1^{\alpha }}+\frac{1}{2^{\alpha }}+...+\frac{1}{n^{\alpha }}$

1 ) Tu dois prouver que :

a) Pour $\alpha =1$, la suite est divergente ( vers +$\infty$)
C'est la suite "harmonique"
Tu as deux démonstrations ici :

https://www.youtube.com/watch?v=yr5nQyGuPT4

b) Pour $\alpha <1$, la suite est divergente ( vers +$\infty$)
Tu peux prouver que cette suite est supérieure à la série harmonique.
Vu que la série harmonique est divergente ( vers +$\infty$), à forciori, celle-ci aussi

c) Pour $\alpha >1$, la suite est convergente
Tu as une explication ici, par comparaison avec une intégrale
http://serge.mehl.free.fr/anx/cv_riemann.html

2 ) Pour un encadrement ( dans le cas $\alpha >1$) , la suite est croissante et majorée par $\frac{\alpha }{\alpha -1}$ , tu peux utiliser cette valeur pour majorer.
Pour minorer, tu as le choix. Le plus simple est de prendre 1.

3 ) "géographiquement" ? tu as peut-être voulu parler de "graphiquement"
Le graphique précédent (partie jaune ) me parait convenir.

[Wil Fried]

@mtschoon J'ai pas compris le 1-c svp.

[mtschoon]

@Wil-Fried ,

J'essaie de t'expliquer le 1)c) par comparaison des aires, pour $\alpha >1$, mais ce n'est pas facile à expliquer....

Je ne sais pas si c'est la méthode ou le calcul qui te pose problème.
Je détaille les deux.

J’utilise les notations de ton énoncé.
Je joins un nouveau graphique où j’ai supprimé les u1,u2,...du lien, car ils étaient très ambigus (et c’est peut-être pour cela que tu n’as pas compris)

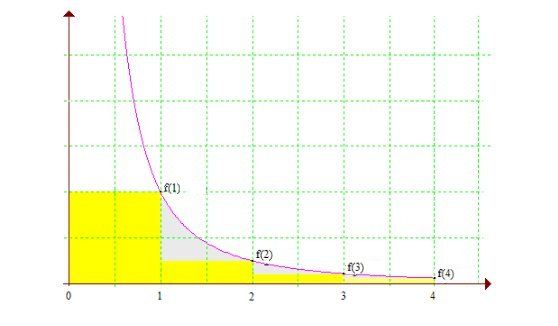
La courbe en rose est la représentation graphique de la.fonction f définie par $\boxed{f(x)=\frac{1}{x^{\alpha }}}$, pour $x>0$ (f est strictement décroissante)

Pour $n\ge 1$ :
$\boxed{U_n=\sum _{k=1}^n\frac{1}{x^{\alpha }}}$
$\boxed{U_n=1+\frac{1}{2^{\alpha }}+\frac{1}{3^{\alpha }}...+\frac{1}{n^{\alpha }}}$

Pour $k=1$ : $1$ = l'aire du carré jaune de gauche (1 en "abscisse" et 1 en "ordonnée")

Pour $k=2$ : $\frac{1}{2^{\alpha }}$= l'aire du premier rectangle de gauche (2-1=1 en "abscisse" et $\frac{1}{2^{\alpha }}=f(2)$ en "ordonnée")

Pour $k=3$ : $\frac{1}{3^{\alpha }}$= l'aire du second rectangle de gauche (3-2=1 en "abscisse" et $\frac{1}{2^{\alpha }}=f(3)$ en "ordonnée")

...
...
etc, jusqu'à $k=n$

La somme des aires de ces rectangles est inférieure à l'aire "sous la courbe" (c'est à dire l'intégrale) :
$\frac{1}{2^{\alpha }}+\frac{1}{3\alpha }+...+\frac{1}{n^{\alpha }}\le {\int }_1^{n}f(x)dx$ c'est à dire
$\frac{1}{2^{\alpha }}+\frac{1}{3\alpha }+...+\frac{1}{n^{\alpha }}\le {\int }_1^n\frac{1}{x^{\alpha }}dx$

En ajoutant 1 à chaque membre :
$1+\frac{1}{2^{\alpha }}+\frac{1}{3\alpha }+...+\frac{1}{n^{\alpha }}\le 1+{\int }_1^n\frac{1}{x^{\alpha }}dx$

$\boxed{U_n\le 1+{\int }_1^n\frac{1}{x^{\alpha }}dx}$

[mtschoon]

Reste à faire le calcul intégral :

$1+{\int }_1^n\frac{1}{x^{\alpha }}dx=1+{\int }_1^n{x}^{-\alpha }dx=1+[\frac{x^{-\alpha +1}}{-\alpha +1}{]}_1^n$

Après calcul , réduction au même dénominateur et simplification, tu dois trouver :
$1+{\int }_1^n\frac{1}{x^{\alpha }}dx=\frac{n^{-\alpha +1}-\alpha }{-\alpha +1}$

Conclusion :
$U_n\le \frac{n^{-\alpha +1}-\alpha }{-\alpha +1}$

C'est à dire : $U_n\le \frac{\alpha -n^{-\alpha +1}}{\alpha -1}$

$(U_n)$ est croissante et majorée par $\frac{\alpha }{\alpha -1}$, donc convergente.