vitesse moyenne et curviligne, temps, distance

bonsoir!
j'ai des difficulté a répondre a cette exercices. Pouvez vous m'aidez svp?
consigne
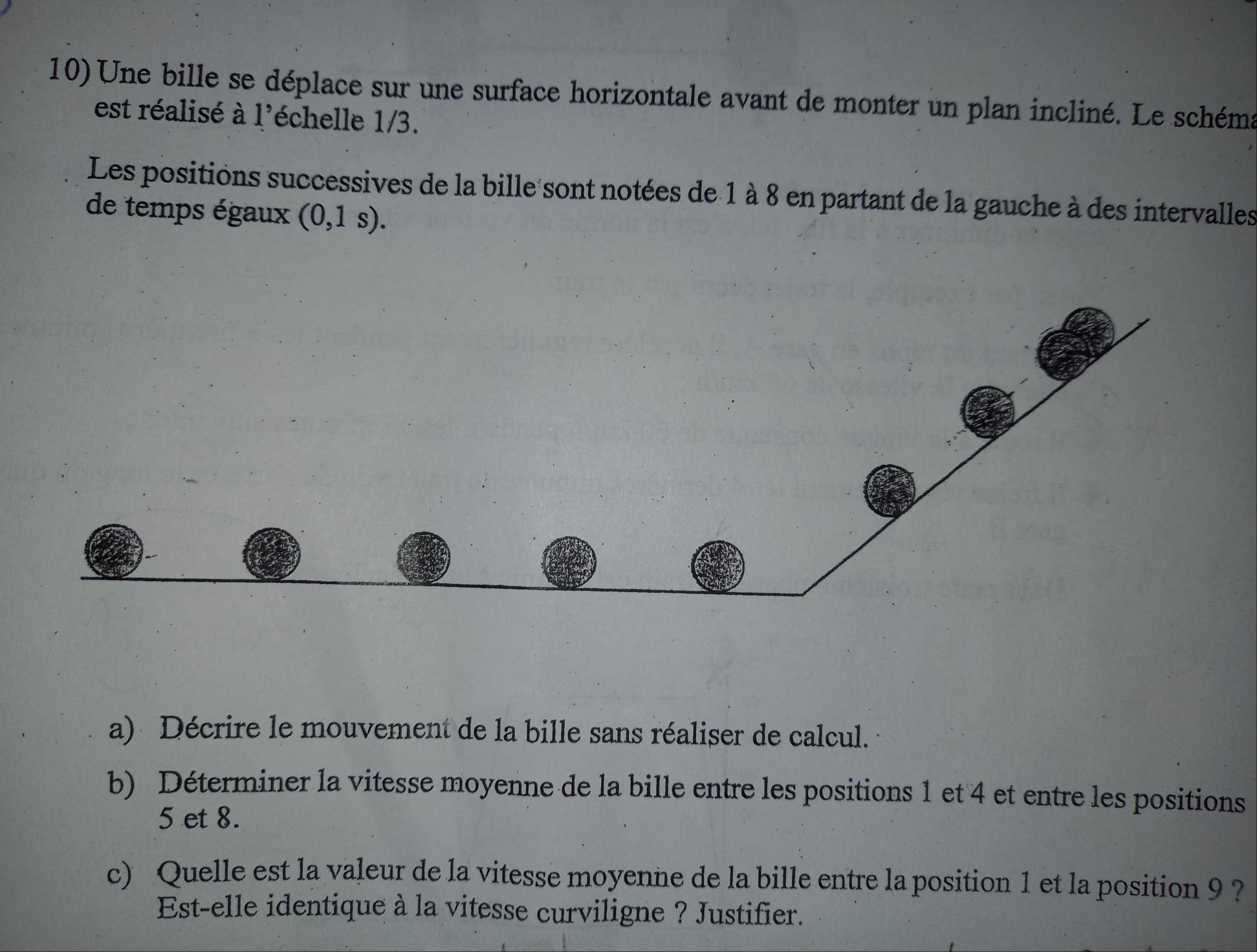
une bille se déplace sur une surface horizontale avant de monter un plan incliné. Le schéma est réalisé à l'échelle 1/3.
les positions successive de la bille sont notées de 1 à 8 en partant de la gauche à des intervalles de temps égaux (0,1s).

a) Décrire le mouvement de la bille sans réaliser de calcul
b) Déterminer la vitesse moyenne de la bille entre les positions 1 et 4 et entre les positions 5 et 8?
c)Quelle est la valeur de la vitesse moyenne de la bille entre la position 1 et la position 9?
Est-elle identique à la vitesse curviligne? justifier.

a) je pense que c'est un mouvement rectiligne uniforme.

@Joyca-Le-Boss Bonsoir,

As-tu mesuré la distance parcourue entre deux positions successives ?

@Noemi
b) j'ai utiliser la formule vitesse moyenne =delta X/delta T <=> 1/3/0,4 = 0,13 m/s (entre les positions 1 et 4)
non je vais le faire maintenant pour la distance parcourue

Bonjour,

Celui qui a fait le dessin a travaillé comme un cochon.

Je présume que sur la partie horizontale, on a un MRU, mais alors les distances entre 2 positions consécutives devraient être toutes les mêmes sur cette partie... et ce n'est clairement pas le cas.

De plus, la distance entre les positions de la bille juste avant et après le coin de la piste devrait être plus petite que entre 2 positions consécutives sur la partie horizontale et ce n'est pas le cas sur le dessin, c'est même le contraire.

On parle aussi de positions successives notées de 1 à 8 ... mais il y a 9 positions sur le dessin.

Evaluer les vitesses par mesures sur le dessin sans avoir le dessin en vraie grandeur est aussi impossible (avec l'échelle donnée et le dessin sur papier, on peut, mais pas sur un écran de PC où on ne connait pas la vraie grandeur du dessin)

Bref, rien de bon dans cet énoncé et son dessin mal foutu.

@Black-Jack bonsoir,
je n'ai fait que recopier l'énoncé et le dessin qui était dans mon dossier d'exercices, avec le même nombres de billes, et presque les mêmes proportions!

@Joyca-Le-Boss

Que veux tu dire quand tu écris : "presque les mêmes proportions" ?

@Noemi c'est a dire l'inclinaison du plan incliné et environ les position des billes.

@Joyca-Le-Boss

Il faut transmettre une photographie du schéma correspondant à l'énoncé.

@Noemi

@Noemi j'ai fait ca , est ce correct? (je ne suis pas sur de mes reponses)

@Joyca-Le-Boss

Sur la partie rectiligne, le mouvement est rectiligne uniforme car les positions des billes sont régulièrement espacées.
Sur la partie inclinée, le mouvement est décéléré car .....

En supposant que la première position est celle de départ donc position 0, mesure la distance entre la bille en position 1 et 4 et tu divises par le temps, soit $3×0,13\times 0,1$ s
Tiens compte de l'échelle.

@Noemi j'ai fait 1/3 . 6, cela me donne 2
{6 étant la mesure a la latte de la position (1 à4)}
vitesse moyenne = 2/3.0,1 => 6,6 m/s
Est ce juste?

@Joyca-Le-Boss

Quelle est l'unité de 6 la mesure entre la bille 1 et la bille 4 ?

@Noemi comme c'est a la latte (en cm)

@Joyca-Le-Boss

Donc la vitesse moyenne, en cm/s, sur la partie horizontale est :
$\dfrac{6}{0,3}= ....$

Applique le même calcul pour la partie inclinée.

@Noemi désolé mais la prof n'a pas indiquer d'unité à utiliser , on va donc utiliser le mètre comme unité de référence qui est plus simple à utiliser. donc 6m/0,3 = 6,6m/s est ce correct

@Joyca-Le-Boss

Tu dois utiliser l'échelle et l'unité du graphique.

Vérifie le calcul 6/0,3 = 20 !

@Noemi ah oui desole merci

@Joyca-Le-Boss
b) 5/0,3 => 16,6cm/s positions 5 et 8
est ce correcte maintenant ?

@Joyca-Le-Boss

Je ne peux pas vérifier le 5 et le 6 cm.
L'unité est pour moi le cm/s.

@Noemi
14/0,7 => 20cm/s

0,1.7= 0,7 sec

@Joyca-Le-Boss

Dans tous les calculs, tu n'as pas pris en compte l'échelle 1/3 du schéma.
Si tu mesures 5 cm, cela donne 15 cm en réalité.

Rectifie les calculs.

@Joyca-Le-Boss dsl j'ai diviser par 0,3 et non par 1/3
je dois faire la même chose pour les autres?

@Noemi en effet cela donne bien 5/1/3 =15

@Joyca-Le-Boss

Il faut diviser par 0,3 car cela correspond au temps.
C'est la mesure que tu multiplies par 3, pour avoir la distance réelle.

@Noemi desolé j'ai pas compris

@Joyca-Le-Boss

Le schéma est à l'échelle 1/3, donc il faut multiplier les mesures effectuées par 3 pour avoir la valeur réelle.

@Noemi donc ici 15.3 =45 cm/s

@Noemi faut il faire la même chose? avec
6/1/3.3=54

@Noemi et pour la question c je ne comprends pas, sachant qu'on n'a pas du tout aborder ce sujet (vitesse curviligne) en classe)

Quelle est la valeur de la vitesse moyenne de la bille entre les positions 1 et 9?
Est-elle identique a la vitesse curviligne? justifier

@Joyca-Le-Boss

Je reprends,

La distance que tu as mesurée entre les billes 1 et 4 est 6 cm.
Comme l'échelle est 1/3, la distance réelle est $6×3=186\times 3 = 18$ cm.

Entre la bille 1 et la bille 4, 3 intervalles de temps donc
$3\times 0,1 = 0,3$ s

La vitesse moyenne pour la partie horizontale est : $\dfrac{18}{0,3}= 60$ cm/s

Revois le calcul pour la partie inclinée.

Bonjour,

Remarque (à oublier pour ne pas perturber Joyca Le Boss) ... mais qui devrait titiller celui qui a pondu l'exercice et n'a visiblement aucune compétence en Physique.

Si la vitesse sur la partie horizontale est vraiment de 0,6 m/s, alors on pourrait (en se trompant un peu) calculer la hauteur maximale atteinte sur la pente, on aurait h = vo²/(2g) = 0,6²/(2*9,81) = 0,018 m (1,8 cm), alors que sur le dessin la mesure de h est d'environ 10 cm ???

Ce qui est calculé ci-dessus serait correct si le mobile glissait sans rouler et sans frottement.

Si (hors de connaissance en Secondaire), on tient compte que la bille roule et ne glisse pas, avec une bille pleine et homogène, on trouverait une hauteur plus élevée (par l'énergie cinétique de rotation de la bille), et on aurait h = 0,7 * vo²/g = 0,7 * 0,6²/9,81 = 0,026 m (2,6 cm)

Et si on considère une bille creuse ... on aurait h encore un peu plus grand (je vous épargne le calcul) ... mais quoi qu'il en soit, la hauteur maximale atteinte serait et de très très loin inférieure à celle qu'on peut mesurer (en tenant compte de l'échelle) sur le dessin.

Si on veut que le problème s'approche de quelque chose de possible, il faut que l'expérience soit sur un astre avec une accélération de la pesanteur très en dessous de celle sur la Terre, pourquoi pas évidemment ... mais alors il vaut mieux le préciser.

Certains rétorqueront que ce n'est qu'un exercice de math ... et bien ce n'est pas une raison. Si c'est pour donner des exercices avec des résultats physiques complètement idiots, il vaut mieux s'abstenir, A part donner un très mauvais ressenti des phénomènes physiques à l'élève, cela n'apporte pas grand chose.