Nombres complexes et transformations plane
-
MMohssine dernière édition par Mohssine
Bonjour,
Le plan complexe est rapporté à un repère orthonormé direct.
décrit la transformation dont l'écriture complexe est z'= -e^(2iπ/3)z +1
-
MMohssine dernière édition par
@Mohssine en cours on a z' est une rotation de centre Omega si z'-w=eiθ(z-w)
-
mtschoon dernière édition par mtschoon

@Mohssine , bonjour,
Effectivement, la transformation proposée est bien une rotation.
Si j'ai bien lu :
z′=−e2iπ3z+1z'=-e^{\dfrac{2i\pi}{3}}z+1z′=−e32iπz+1
Il faut que tu transformes le "-"
z′=(−1)e2iπ3z+1z'=(-1)e^{\dfrac{2i\pi}{3}}z+1z′=(−1)e32iπz+1
−1=eiπ-1=e^{i\pi}−1=eiπ donc :
z′=(eiπ)e2iπ3z+1z'=(e^{i\pi})e^{\dfrac{2i\pi}{3}}z+1z′=(eiπ)e32iπz+1
En ajoutant les exposants :
z′=e5iπ3z+1\boxed{z'=e^{\dfrac{5i\pi}{3}}z+1}z′=e35iπz+1
-
mtschoon dernière édition par mtschoon

Si tu préfères :
5π3=−π3[2π]\dfrac{5\pi}{3}=-\dfrac{\pi}{3} [2\pi]35π=−3π[2π]
z′=e−iπ3z+1\boxed{z'=e^{-i\dfrac{\pi}{3}}z+1}z′=e−i3πz+1
-
MMohssine dernière édition par
@mtschoon non je vois pas encore ni l angle ni le centre de la transformation
-
mtschoon dernière édition par mtschoon

@Mohssine , nos derniers messages ont dû de se croiser...
-
MMohssine dernière édition par
@mtschoon mais t as pas le meme w dans cette expression
-
MMohssine dernière édition par
@Mohssine en cours on doit avoir le meme w z'-w=eiθ(z-w)
-
mtschoon dernière édition par mtschoon

Pour trouver www , effectivement, tu ne peux pas l'avoir immédiatement, vu qu'en factorisant "naturellement" on ne trouve pas le même www, comme tu l'indiques
Il faut s'y prendre autrement.
www étant l'affixe du point invariant, vu que l'image de www est www, tu trouves www en résolvant :
w=e5iπ3w+1w=e^{\dfrac{5i\pi}{3}}w+1w=e35iπw+1
-
MMohssine dernière édition par
@mtschoon on attend naoemi il a peut etre la solution
-
mtschoon dernière édition par mtschoon

@Mohssine , pas de problème pour la solution !
Je complète pour trouver www
Tu peux écrire :
w(1−e5iπ3)=1w(1-e^{\dfrac{5i\pi}{3}})=1w(1−e35iπ)=1
c'est à dire
w=11−e5iπ3w=\dfrac{1}{1-e^{\dfrac{5i\pi}{3}} }w=1−e35iπ1
e5iπ3=cos(5π3)+isin(5π3)=12−32ie^{\dfrac{5i\pi}{3}}=cos(\dfrac{5\pi}{3})+isin(\dfrac{5\pi}{3})=\dfrac{1}{2}-\dfrac{\sqrt 3}{2}ie35iπ=cos(35π)+isin(35π)=21−23i
d'où ;
w=11+32iw=\dfrac{1}{1+\dfrac{\sqrt 3}{2}i}w=1+23i1
En multipliant et divisant par le complexe conjuqué, tu dois trouver, sauf erreur :
w=12−32i\boxed{w=\dfrac{1}{2}-\dfrac{\sqrt 3}{2}i}w=21−23iLe centre Ω\OmegaΩ de la rotation a donc pour coordonnées : (12,−32)(\dfrac{1}{2},-\dfrac{\sqrt 3}{2})(21,−23)
Il aurait été heureux que ton cours t'indique que pour z′=eiθz+bz'=e^{i \theta}z+bz′=eiθz+b, il s'agit de la rotation de centre Ω\OmegaΩ d'affixe www (invariant) et d'angle θ\thetaθ
Tu peux donc conclure.
-
MMohssine dernière édition par
@mtschoon surement il y a une erreur dans cette réponse
-
mtschoon dernière édition par mtschoon

@Mohssine , explique ce que tu veux dire précisemment.
Vois-tu une erreur de calcul ? Si c'est le cas, il faut la donner. Tout est possible, bien sûr !Principe (Théorème) :
z′=az+bz'=az+bz′=az+b avec a=eiθa=e^{i\theta}a=eiθest la forme complexe de la rotation d'angle θ\thetaθ et de centre d'affixe w=b1−aw=\dfrac{b}{1-a}w=1−ab
-
MMohssine dernière édition par
@mtschoon avec les nombres complexes la simplicité doit etre présente
-
mtschoon dernière édition par mtschoon

La simplification doit être présente partout...
Fait une vérification .
z′−w=eiθ(z−w)z'-w=e^{i\theta}(z-w)z′−w=eiθ(z−w) <=> z′=eiθz+w(1−eiθ)z'=e^{i\theta}z+w(1-e^{i\theta})z′=eiθz+w(1−eiθ)
Ici, tu as donc θ=5π3\theta=\dfrac{5\pi}{3}θ=35π et w(1−eiθ)=1w(1-e^{i\theta})=1w(1−eiθ)=1 c'est à dire :
w=11−eiθw=\dfrac{1}{1-e^{i\theta}}w=1−eiθ1C'est le calcul que je t'ai proposé (vu que l'énoncé n'était pas de la forme de ton cours ) et vérifie le calcul si tu as un doute.
Bons calculs .
-
MMohssine dernière édition par
@mtschoon je vais essayer de trouver la réponse pour ca sans doute c est pas un grand exo
-
mtschoon dernière édition par mtschoon

@Mohssine , ce n'était pas un exercice "compliqué", mais ce n'était pas commode vu que la formule de ton cours (Il semble que tu n'en avais qu'une) ne pouvait pas s'appliquer directement.
Je viens de vérifier les calculs proposés vu que tu avais un doute. Pas d'erreur en vue...
Bon travail !
-
mtschoon dernière édition par mtschoon

Illustration graphique
Le centre de la rotation est Ω(12,−32)\Omega (\dfrac{1}{2},-\dfrac{\sqrt 3}{2})Ω(21,−23)
L'angle de la rotation est 5π3=−π3 [2π]\dfrac{5\pi}{3}=\dfrac{-\pi}{3}\ [2\pi]35π=3−π [2π]Pour z=0z=0z=0 (point OOO), z′=1z'=1z′=1 (point O′O'O′)
L'image de OOO est O′O'O′ défini par :
ΩO=ΩO′\Omega O=\Omega O'ΩO=ΩO′ et (ΩO→,(ΩO′→)=−π3 [2π](\overrightarrow{\Omega O},(\overrightarrow{\Omega O'})=\dfrac{-\pi}{3}\ [2\pi](ΩO,(ΩO′)=3−π [2π]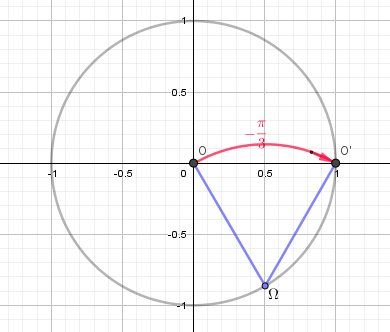
-
MMohssine dernière édition par
@mtschoon la j ai tous compris merci bcp
-
mtschoon dernière édition par

Si tu as tout compris maintenant, c'est parfait @Mohssine !