Vitesse, distance, heure de rencontre

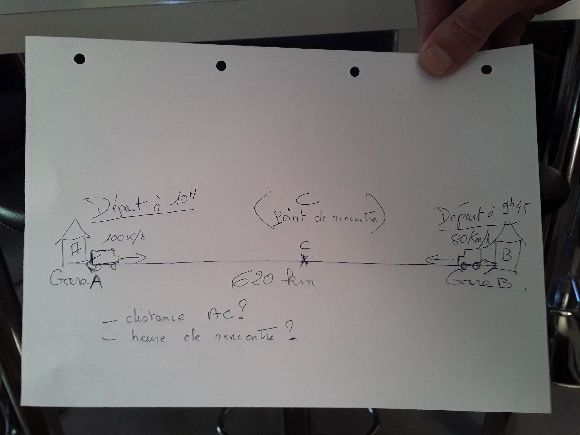
Pouvez vous m'aider . Merci

@nanachouchetta Bonjour (Marque de politesse à ne pas oublier !!)

Le schéma est difficile à lire. N'y a t'il pas un énoncé que tu dois écrire.

Bonjour désolé non j'ai juste ça . Merci

@nanachouchetta

En utilisant la relation pour la vitesse moyenne : $\dfrac{d}{t}$
Ecris la distance parcourue par chaque véhicule.
$x$ est la distance parcourue en km et $t$ la durée du parcours en heure.
Départ du point A : distance parcourue $xA=100×tAx_A=100\times t_A$
Départ du point B : distance parcourue $xB=80×tBx_B=80\times t_B$
et au moment de la rencontre : $tB=tA+1560t_B= t_A+\dfrac{15}{60}$ et $x_A = 620-x_B$

Je te laisse poursuivre.
Indique tes calculs et/ou résultats si tu souhaites une vérification.

@Noemi bonjour je vous transmets ce que j'ai trouvé . Cordialement .

@nanachouchetta

C'est correct, tu peux calculer la distance AC.

bonjour les amis, en faite je ne pense que ce que vous avez fait soit correcte:
pour les équations horaire d'un mouvement rectiligne uniforme il faut dabord choisir l'origine du repère et puis choisir l"origine de la date et puis etablir les formules comme suite: x(t)=v*(t-t0) + x0 avec x0 et t0 comme origine respectivement origine du repere et origine de la date.

@tiftaf a dit dans Vitesse, distance, heure de rencontre :

bonjour les amis, en faite je ne pense que ce que vous avez fait soit correcte:
pour les équations horaire d'un mouvement rectiligne uniforme il faut dabord choisir l'origine du repère et puis choisir l"origine de la date et puis etablir les formules comme suite: x(t)=v*(t-t0) + x0 avec x0 et t0 comme origine respectivement origine du repere et origine de la date.

Mais si c'est correct,

Bonjour,

Les résultats trouvés par nanachouchetta sont corrects ... mais il manque le calcul de la distance AC

A 10h le véhicule B a parcouru 80 * 0,25 = 20 km
Il reste donc, à cet instant, une distance de 620 - 20 = 600 km entre les véhicules

La vitesse relative entre les véhicules à partir de 10 h est v = 100 + 80 = 180 km/h

Les véhicules se croiseront donc après une durée (mesurée à partir de 10 h) t = 600/180 h soit 3h 20min

L'heure de croisement est donc 13h 20min

On a donc AC = 100 * 600/180 = 333,33 km (arrondi)

@titaf,

Rebonjour,

On peut évidemment résoudre le problème, en choisissant un repère d'espace et une horloge et écrire les équations des mouvements des 2 véhicules et ...
Mais, on doit arriver aux mêmes résultats pour répondre aux questions posées (heure de croisement et distance AC) que par la méthode utilisée dans ma réponse précédente ou par celle utilisée par nanachouchetta ... qui est d'ailleurs équivalente à celle que j'ai utilisée.

On aurait alors, par exemple ceci :

Origine d'horloge : 9,75 h
unité : 1 heure

Axe des abscisses : droite(AB) (graduée en km)
origine : point A

xB(t) = 620 - 80*t
xA(t) = 100 * (t - 0,25) (pour t >= 0,25)

Croisement pour xA = xB, soit pour : 620 - 80*t = 100 * (t - 0,25)
620 - 80t = 100t - 25
t = 645/180

heure de croisement : 9,75 + 645/180 = 40/3 h (soit 13h 20min)

et xA(40/3) = 100 * (645/180 - 0,25) = 333,33 km (arrondi) ... qui est la distance [AC]