Exercice sur le produit scalaire
-
Ttiti.gn dernière édition par
Bonjour,
J’aurai s’il vous plaît besoin d’aide pour cet exercice.ABDC est un rectangle de longueur AB=6 et de largeur AC=4
E est un point du segment AB défini par le vecteur AE= 1/4 de du vecteur AB
F est je projeter orthogonal du point B sur la droite ED.
A) en calculant le produit scalaire de EC.ED de deux façon différentes, calculer l’angle DEC.
B) en calculant le produit scalaire DB.DE de deux façon différentes, calculer la longueur BF.Je suis vraiment bloquer la dessus je ne sais pas comment le résoudre.
Merci d’avance.
-
mtschoon dernière édition par mtschoon

@titi-gn , bonjour,
Vérifie ton énoncé.
Tu as écrit :
"ABDC est un rectangle de longueur AB=6 et de largeur AC=4"J'ai un doute.
N'est-ce pas plutôt BC=4 ?Merci de vérifier.
-
BBlack-Jack dernière édition par
Bonjour,
A)
En supposant que c'est BC = 4 et pas AC = 4 comme tu l'as écrit.
Je fais le 1er (il te faudra quand même bien le comprendre) et te passe la main pour la suite ...
Commence par faire un dessin...
vec(EC).vect(ED) = EC * ED * cos(DEC) (1)
Pythagore dans le triangle EBC ... --> EC = 1/2.V(145) (avec V pour racine carrée)
Pythagore dans le triangle DAE ... --> ED = 1/2.V(73) (avec V pour racine carrée)
vec(EC).vect(ED) = 1/2.V(145)* 1/2.V(73)* cos(DEC)
vec(EC).vect(ED) = 1/4.V(10585) * cos(DEC) (1)mais aussi :
vec(EC).vect(ED) = (vec(EB) + vec(BC)).(vec(EA) + vec(AD))
vec(EC).vect(ED) = vec(EB).vec(EA) + vec(EB).vec(AD) + vec(BC).vec(EA) + vec(BC).vec(AD)
vec(EC).vect(ED) = 3/4 . vec(AB).(-1/4).vec(AB) + 0 + 0 + vec(BC).vec(BC)
vec(EC).vect(ED) = -3/16 * AB² + BC² = -3/16 * 6² + 4²
vec(EC).vect(ED) = 37/4 (2)(1) et (2) --> 1/4.V(10585) * cos(DEC) = 37/4
cos(DEC) = 37/V(10585)
angle(DEC) = 68,92...°A toi de comprendre tout ce qui précède ...
Et ensuite, en appliquant une méthode analogue tu pourras essayer de résoudre le point B de l'exercice.
-
mtschoon dernière édition par mtschoon

Bonjour,
En supposant, bien sûr, que la modification proposée soit bonne, ce qui est fort probable, voici un schéma pour éclairer cet exercice.
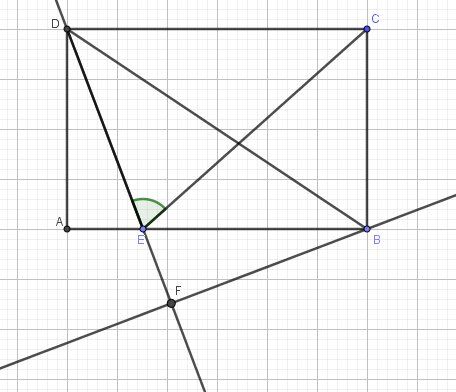
-
mtschoon dernière édition par mtschoon

@titi-gn , je te donne quelques indications pour le B) (Toujours en supposant que la modification proposée est bonne),
Je me demande encore si il n’y a pas une autre faute dans ton énoncé donné.
Est-ce vraiment BF qu’il faut calculer ? N’est-ce pas DF ?
De toute façon, après avoir calculer DF, tu peux trouver BF sans difficulté (si c’est la question)Je t'indique seulement des pistes ; à toi de faire les calculs.
Une façon en décomposant les vecteurs avec la relation de Chasles
DB→.DE→=(DA→+AB→).(DA→+AE→)\overrightarrow{DB}.\overrightarrow{DE}=(\overrightarrow{DA}+\overrightarrow{AB}).(\overrightarrow{DA}+\overrightarrow{AE})DB.DE=(DA+AB).(DA+AE)
Tu développes.
Deux produits scalaires seront nuls ( car vecteurs orthogonaux) et les deux autres sont simples à calculer.Une autre façon en utilisant le théorème sur la projection (voir cours)
DB→.DE→=DF→.DE→\overrightarrow{DB}.\overrightarrow{DE}=\overrightarrow{DF}.\overrightarrow{DE}DB.DE=DF.DE
donc
DB→.DE→=DF×DE×cos0=DF×DE\overrightarrow{DB}.\overrightarrow{DE}=DF\times DE\times cos0=DF\times DEDB.DE=DF×DE×cos0=DF×DEEn identifiant ces deux expressions de DB→.DE→\overrightarrow{DB}.\overrightarrow{DE}DB.DE, tu obtiendras la valeur de DFDFDF.
Si BFBFBF est demandé, tu peux le déduire en utilisant le Théorème de Pythagore .Tu peux donner tes réponses sit tu souhaites une vérification.