Analyse : Une seule droite tangente à la courbe
-
Jérémie dernière édition par Noemi
Bonjour je ne sais pas comment faire cet exercice. Je ne sais pas si ma démarche est la bonne. Cet exercice mélange les chapitres Dérivabilité ; Convexité/Continuité.
Soit f une fonction définie sur ]0.5 ; plus l'infini [ par f(x)= ✓(2x-1) et C sa courbe représentative dans un repère du plan. Démontrer qu'il n'existe qu'une seule et unique droite qui soit Tengente à C et qui passe par l'origine.
J'ai d'abord dérivée la fonction f puisqu'on étudié sa Tengente. f'(x) = -1/ ✓(2x-1). L'ensemble de définition de f' est R {1/2}.
Puis je pense qu'il faut écrire l'expression réduite de la Tengente à la courbe. Ta : y= f'(a)(x-a)+f(a)
Après je ne sais pas quoi faire : S'il faut étudier la convexité de f grâce au sens de variation de f' ?Merci de votre aide
-
mtschoon dernière édition par mtschoon

@Jérémie , bonjour,
Revois la dérivée. Tu dois trouver (après simplification par 2) f′(x)=12x−1f'(x)=\dfrac{1}{\sqrt{2x-1}}f′(x)=2x−11
Revois l'ensemble de définition de f′f'f′
2x−1>02x-1\gt 02x−1>0<=> x>12x\gt \dfrac{1}{2}x>21
f est dérivable sur ]12,+∞[]\dfrac{1}{2},+\infty[]21,+∞[
L'équation de la tangente en aaa est bien :
y=f′(a)(x−a)+f(a)y=f'(a)(x-a)+f(a)y=f′(a)(x−a)+f(a)
y=12a−1(x−a)+2a−1y=\dfrac{1}{\sqrt{2a-1}}(x-a)+\sqrt{2a-1}y=2a−11(x−a)+2a−1
Pour que la tangente passe par l'origine, pour x=0x=0x=0, y=0y=0y=0
0=12a−1(−a)+2a−10=\dfrac{1}{\sqrt{2a-1}}(-a)+\sqrt{2a-1}0=2a−11(−a)+2a−1
Tu as une équation d'inconnue aaa à résoudre.
Essaie de poursuivre.
-
Jérémie dernière édition par
La dérivée est bien 1/✓(2x-1)
Ta : y = f'(a)(x-a)+f(a)
Soit pour x=0 et y= 0 :
1/✓(2a-1) * (-a) + ✓(2a-1) = 0
Équivalent à -a/✓(2a-1) + ✓(2a-1) = 0
Équivalent à -a +2 ✓(a-1) /✓(2a-1) = 0
Équivalent à a-1/ ✓(2a-1) = 0
✓(X) est toujours > 0 en plus c'est le dénominateur
Donc a-1 = 0 soit a=1Je fais quoi de ce résultat ?
-
Jérémie dernière édition par
Si on remplace a par 1 on obtient la droite d'équation y=x qui est la Tengente à la courbe au point d'abscisse 1.
Je ne suis pas sûr que ce soit cohérent ?
-
mtschoon dernière édition par mtschoon

@Jérémie ,
Ton calcul est bon.
C'est bien a=1a=1a=1Il te reste à remplacer aaa par 111 dans l'équation de la tangente ;
Sauf erreur, tu dois trouver y=xy=xy=xIllustration graphique :
La courbe est en rouge
La tangente est en bleu.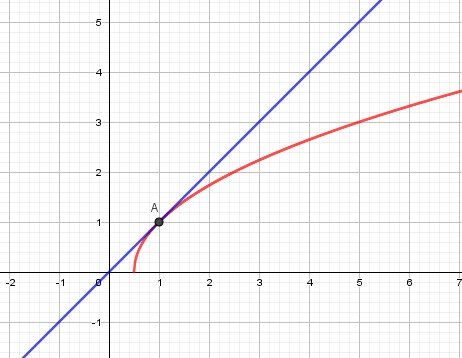
-
mtschoon dernière édition par

-
Jérémie dernière édition par
@mtschoon
D'accord Merci de m'avoir débloqué
-
mtschoon dernière édition par

@Jérémie , de rien !
A+