Probabilité statistiques licence 2

[saliou1]

Un chasseur tire sur un animal qui essaye de se cacher . Mais le chasseur ne peut que faire 4 tirs indépendants . Les probabilités d'atteindre l'animal dans ces tirs sont respectivements : 0,6; 0,5;0,4;03.
Soit x la variable aléatoire discrète << nombre de tirs faits>>.
Nb: le tir est arrêté dès que la cible est atteinte.
Trouver:

1. la Loi de distribution de la variable aléatoire x.
2. E(x), Var(x) et l'écart-type de x.
3. la probabilité pour que le chasseur fasse au plus 2 tirs.
4. p(x >= 3).
5. p(1<x=<3).
   Je demande une aide de préférence d'ici vendredi soir.

[Noemi]

@saliou1 Bonjour,(Marque de politesse à ne pas oublier !!)

Indique la question qui te pose problème.
Tu peux construire un arbre pour déterminer la loi de distribution.

[mtschoon]

Bonjour,

@saliou1 , je te mets un arbre pour clarifier la situation.

Le point de départ est en rouge .
$S$ veut dire : la cible est atteinte (c'est un Succès)
$\overline{S}$ veut dire : la cible n'est pas atteinte (c'est un échec)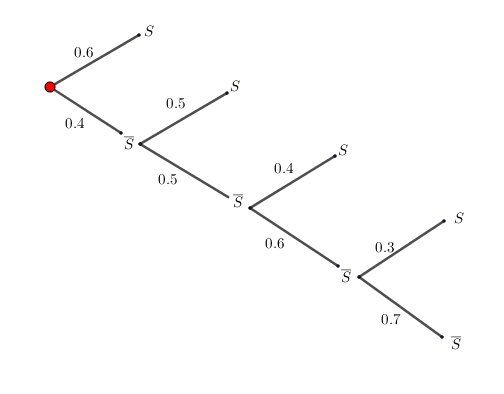

Comprends bien l'arbre, et ensuite, essaie de donner la loi de distribution de X
Les autres questions s'en déduisent directement.

[mtschoon]

@saliou1 , pour que tu puisses vérifier tes réponses, je t'indique ce que tu dois trouver à la loi de distribution de X :
$P(X=1)=0.6$
$P(X=2)=0.2$
$P(X=3)=0.08$
$P(X=4)=0.12$

Tu peux t'assurer que la somme des probabilité vaut bien 1
$0.6+0.2+0.08+0.12=1$

Reposte si tu n'arrives pas à trouver ces valeurs.