SVP j ai besoin d aide dans un exercice d isométrie
-
Mariem jabloun dernière édition par Mariem jabloun
Bonjour
j ai des difficultés a repondre a la question suivante
Énoncé
ABCD un carre direct
E un point de [AB] prive de A et B
la droite parallele a (BD) et passante par E coupe la droite (BC) en F
E=R(D,pi/2)(G)
soit g=S(BD)oSc
H=S(BD) (G)
L=Sc(H)
Montrer que (BD) est la mediatrice de [LF]?
-
mtschoon dernière édition par mtschoon

@Mariem-jabloun , bonjour,
Visiblement, tu n'as pas donné ton énoncé en entier.
Il semble que ce soit la fin d'un exercice.
g=S(BD)oSc n'aide guère...Il y a certainement des résultats trouvés aux questions précédentes utiles pour celle que tu poses. Dommage...
Alors, je te donne des pistes, mais incomplètes...
Schéma :
(le cercle est seulement un outil de constrution; il ne sert pas pour la démonstration)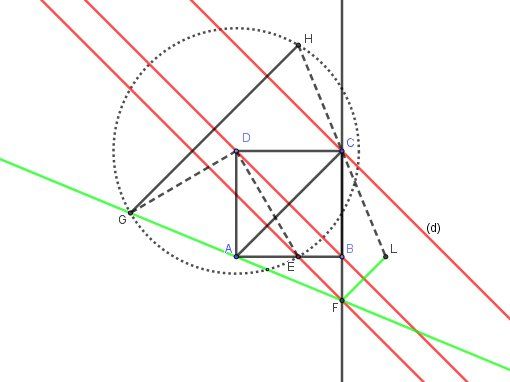
-
mtschoon dernière édition par mtschoon

Pour répondre à ta question "(BD) est la médiatrice de [LF]" , il faut trouver que L=S(BD)(F)\boxed{L=S_{(BD)}(F)}L=S(BD)(F) en "jonglant" avec les transformations...
Remarque : comme la loi o est associative, je ne mets pas de parenthèses pour alléger les écritures.
Pistes,
L=SC(H)=SCoS(BD)(G)L=S_C(H)=S_CoS_{(BD)}(G)L=SC(H)=SCoS(BD)(G)
Or, graphiquement, on constate que GGG est le symétrique de FFF par SAS_ASA
J'imagine que cela a été prouvé dans une question précédente.
Donc :
L=SC(H)=SCoS(BD)oSA(F)L=S_C(H)=S_CoS_{(BD)}oS_A(F)L=SC(H)=SCoS(BD)oSA(F)
SCS_CSC peut se décomposer en deux symétries axiales.
Soit (d)(d)(d) la droite passant par CCC et perpendiculaire à (AC)(AC)(AC)
SC=S(d)oS(AC)S_C= S_{(d)}oS_{(AC)}SC=S(d)oS(AC)
Donc :
L=SC(H)=S(d)oS(AC)oS(BD)oSA(F)L=S_C(H)=S_{(d)}o S_{(AC)}oS_{(BD)}oS_A(F)L=SC(H)=S(d)oS(AC)oS(BD)oSA(F)
Or,
S(AC)oS(BD)=SOS_{(AC)}oS_{(BD)}=S_OS(AC)oS(BD)=SO
Donc
L=SC(H)=S(d) o SO o SA(F)L=S_C(H)=S_{(d)}\ o \ S_O \ o\ S_A(F)L=SC(H)=S(d) o SO o SA(F)
Or,
SO SA=TAC→=S(d)oS(BD)S_O \ S_A=T_{\overrightarrow{AC}}=S_{(d)}oS_{(BD)}SO SA=TAC=S(d)oS(BD)
J'imagine aussi que cela a été prouvé dans une question précédente.
Donc :
L=SC(H)=S(d)oS(d)oS(BD)(F)L=S_C(H)=S_{(d)}oS_{(d)}oS_{(BD)}(F)L=SC(H)=S(d)oS(d)oS(BD)(F)
Or,
S(d)oS(d)=IdS_{(d)}oS_{(d)}=IdS(d)oS(d)=Id (application identique)Au final :
L=S(BD)(F)\boxed{L=S_{(BD})(F)}L=S(BD)(F)
(BD) est médiatrice de [LF]Revois tout ça de près et complète ce qui a été dit mais pas démontré dans ces calculs, mais qui doit être fait dans les questions précédentes..
-
BBlack-Jack dernière édition par
@mtschoon a dit dans SVP j ai besoin d aide dans un exercice d isométrie :
@Mariem-jabloun , bonjour,
Visiblement, tu n'as pas donné ton énoncé en entier.
Il semble que ce soit la fin d'un exercice.
g=S(BD)oSc n'aide guère...Il y a certainement des résultats trouvés aux questions précédentes utiles pour celle que tu poses. Dommage...
Alors, je te donne des pistes, mais incomplètes...
Schéma :
(le cercle est seulement un outil de constrution; il ne sert pas pour la démonstration)
Bonjour,
Juste pour savoir ...
Les notations utilisées ici sont différentes de celles que j'utilisais il y a plusieurs décennies et donc, pour être sûr :
Que signifie (avec des mots) : E=R(D,pi/2)(G)
J'aurais pensé que cela signifiait que E se trouvait par la rotation d'un angle Pi/2 du point G autour du point D.
Mais si c'est le cas, alors il y a un soucis, car la rotation de + Pi/2 devrait être dans le sens anti-horlogique (sens positif conventionnel)
Et ton dessin, pour retomber sur le point E, fait tourner G de Pi/2 autour de D dans le sens horlogique.
C'est très probable que cette incompréhension vient de moi ou plutôt des notations actuelles qui ne collent pas avec celles qu'on m'a enseignées il y a très longtemps.
-
mtschoon dernière édition par mtschoon

Bonjour,
Contente que tu t'intéresses au graphique @Black-Jack
J'explicite,
E=R(D,π2)(G)\boxed{E=R(D, \dfrac{\pi}{2})(G)}E=R(D,2π)(G)
Cela signifie que l'image de GGG est EEE par la rotation d'angle π2\dfrac{\pi}{2}2π ***(sens "trigonométrique", inverse des aiguilles d'une montre)
(DG→,DE→)=+π2 [2π](\overrightarrow{DG},\overrightarrow{DE})=+\dfrac{\pi}{2}\ [2\pi](DG,DE)=+2π [2π]donc, réciproquement :
G=R(D,−π2)(E)\boxed{G=R(D, -\dfrac{\pi}{2})(E)}G=R(D,−2π)(E)
Cela signifie que l'image de EEE est GGG par la rotation (réciproque de la précédente) d'angle −π2-\dfrac{\pi}{2}−2π
(DE→,DG→)=−π2 [2π](\overrightarrow{DE},\overrightarrow{DG})=-\dfrac{\pi}{2}\ [2\pi](DE,DG)=−2π [2π]Connaissant EEE sur ]AB[]AB[]AB[ (par hypothèse), c'est ainsi que se place GGG (avec cette rotation "réciproque" d'angle −π2-\dfrac{\pi}{2}−2π )
C'est ce qui a été fait dans le graphique, correspondant à l'énoncé donné.
Bonne journée !
-
BBlack-Jack dernière édition par
@mtschoon a dit dans SVP j ai besoin d aide dans un exercice d isométrie :
Bonjour,
Contente que tu t'intéresses au graphique @Black-Jack
J'explicite,
E=R(D,π2)(G)\boxed{E=R(D, \dfrac{\pi}{2})(G)}E=R(D,2π)(G)
Cela signifie que l'image de GGG est EEE par la rotation d'angle π2\dfrac{\pi}{2}2π ***(sens "trigonométrique", inverse des aiguilles d'une montre)
(DG→,DE→)=+π2 [2π](\overrightarrow{DG},\overrightarrow{DE})=+\dfrac{\pi}{2}\ [2\pi](DG,DE)=+2π [2π]donc, réciproquement :
G=R(D,−π2)(E)\boxed{G=R(D, -\dfrac{\pi}{2})(E)}G=R(D,−2π)(E)
Cela signifie que l'image de EEE est GGG par la rotation (réciproque de la précédente) d'angle −π2-\dfrac{\pi}{2}−2π
(DE→,DG→)=−π2 [2π](\overrightarrow{DE},\overrightarrow{DG})=-\dfrac{\pi}{2}\ [2\pi](DE,DG)=−2π [2π]Connaissant EEE sur ]AB[]AB[]AB[ (par hypothèse), c'est ainsi que se place GGG (avec cette rotation "réciproque" d'angle −π2-\dfrac{\pi}{2}−2π )
C'est ce qui a été fait dans le graphique, correspondant à l'énoncé donné.
Bonne journée !
Merci ...
J'ai souvent du mal à raccrocher les notations utilisées à mon époque (bien lointaine et pas en France) avec celles utilisées aujourd'hui.
La symbolique c'est peut-être beau, mais c'est dommage qu'elle n'est pas universelle. (pas que pour cela, essaie d'utiliser toute la symbolique mathématique européenne outre atlantique ... elle y est inconnue).
J'ai d'ailleurs remarqué en consultant de multiples sites que la plupart préfèrent les phrases à la symbolique, c'est moins concis mais tellement plus clair pour ceux qui ne manipulent pas ces notations fréquemment.
Bonne journée
-
Mariem jabloun dernière édition par
@mtschoon
Bonjour
Et merci beaucoup
oui c est indiqué de montrer que A est le milieu de [GF]
mais ce n est pas demandé de trouver que SooSA=tr=T de vecteur AC
-
mtschoon dernière édition par mtschoon

De rien @Mariem-jabloun,
Pour la translation de vecteur AC→\overrightarrow{AC}AC je pense que tu n'auras pas de problème pour la justification, vu qu'il s'agit de la composée deux symétries axiales avec des axes de symétrie parallèles , perpendiculaires à (AC) (voir cours).
Bon travail !
Une autre fois, donne l'énoncé entier, même si c'est seulement la fin qui te pose problème, pour pouvoir mieux t'aider.