Trigonométrie maths spe
-
Mmik16 dernière édition par
- On sait que 0 ≤ 𝑥 ≤ 𝜋 et que 𝑐𝑜𝑠(𝑥) = 1/3 Déterminer 𝑠𝑖𝑛 (𝑥).
- On sait que 𝜋 ≤ 𝑥 ≤ 2𝜋 et que 𝑠𝑖𝑛(𝑥) = − 1 / racine de 3. Déterminer 𝑐𝑜s (𝑥)
1 – (cosx )^2+(sinx )^2=1
⇔(1/3)^2+(sin(x)²)= 1
⇔(sin(x)²=1-(1/3)²)
⇔(sin(x)²=1- 1/9)
⇔(sin(x)²= 9/9) - 1/9
⇔(sin(x)²= 8/9)
⇔sin(x= √(8/9)) ou sin(x= - √(8/9))
= (2√2)/3 = - (2√2)/3
≈0.94 ≈ - 0.94
2 – (cosx )^2+(sinx )^2=1
⇔(cos〖x)²+(-1/√3)²=1〗
⇔(cos〖x)²+ 1/3=1〗
⇔(cos〖x)²=1- 1/3〗
⇔(cos〖x)²= 3/3〗 - 1/3
⇔(cos〖x)²= 2/3〗
⇔cos〖x= √(2/3)〗 ou cos〖x= - √(2/3)〗
Bonjour, pouvez-vous me dire si cela est correct ? Car je ne sais pas ce que je dois faire avec ''0 ≤ 𝑥 ≤ 𝜋'' et ''𝜋 ≤ 𝑥 ≤ 2𝜋''.
Merci d'avance
-
@mik16 Bonsoir (marque de politesse à ne pas oublier !!)
L'intervalle pour xxx permet de déterminer la solution entre la valeur positive ou négative.
Place les valeurs sur le cercle trigonométrique ou détermine le signe à partir des données de l'énoncé.Attention à la rédaction, par exemple, les crochets dans le deuxième calcul.
-
Mmik16 dernière édition par
Merci, du coup la solution est celle positive ? Étant donné que 𝜋 et 2𝜋 sont positifs?
-
Ce n'est pas la justification.
Pour 0≤x≤π0\leq x\leq \pi0≤x≤π et cos(x)>0cos(x)\gt0cos(x)>0 alors sin(x)>0sin(x)\gt0sin(x)>0
donc
pour cos(x)=13cos(x)=\dfrac{1}{3}cos(x)=31, sin(x)=223sin(x)=\dfrac{2\sqrt2}{3}sin(x)=322.Pour π≤x≤2π\pi\leq x\leq 2\piπ≤x≤2π et sin(x)<0sin(x)\lt0sin(x)<0 alors −1≤cos(x)≤1-1\leq cos(x)\leq 1−1≤cos(x)≤1
donc
....
-
mtschoon dernière édition par mtschoon

Bonjour,
@mik16 ,
Une remarque sur ta façon d'écrire.Regarde comment écrit @Noemi
Tu ne mets pas les parenthèses au bon endroit.
L'écriture sin(x= √(8/9)) est fausse vu que ce n'est pas x qui vaut √(8/9), c'est le sinus de x
Tu dois écrire sin(x)=√(8/9) , ou tout simplement, vu qu'il n'y a pas d'ambiguïté, sin x =√(8/9).
Fais comme ton professeur à l'habitude.je vais te joindre deux schémas , chacun correspondant à une de tes questions.
Le cercle trigonométrique est l'outil de la trigo.
Je te conseille de faire les schémas, pour comprendre , avant de faire les calculs.
Les schémas te permettent d'avoir le signe du sinus et/ou du cosinus souhaité et les valeurs approchées;
Bien sûr, seuls les calculs permettent d'avoir les valeurs exactes.
-
mtschoon dernière édition par mtschoon

Pour la question 1.
xxx est une mesure de l'angle (OA→,OM→)(\overrightarrow{OA}, \overrightarrow{OM})(OA,OM) donc M est forcément sur le demi-cercle rouge.
Pour placer M :
Sur l'axe des abscisses, tu places le point H d'abscisse 13\dfrac{1}{3}31
Par H, tu traces la droite perpendiculaire à l'axe des abscisse qui coupe le demi-cercle rouge en M.
Le projeté de M sur l'axe des ordonnées est K
Le sinus cherché est l'odonnée de M , c'est à dire OK‾\overline{OK}OK qui est positive.
Par lecture graphique : sin(x)≈0.94sin( x)\approx 0.94sin(x)≈0.94
Le calcul t'a permis d'avoir la valeur exacte : sin(x)=223sin(x)=\dfrac{2\sqrt 2}{3}sin(x)=322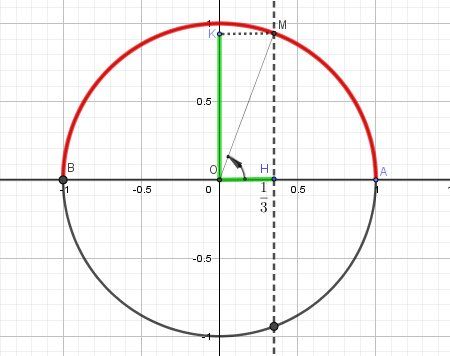
-
mtschoon dernière édition par mtschoon

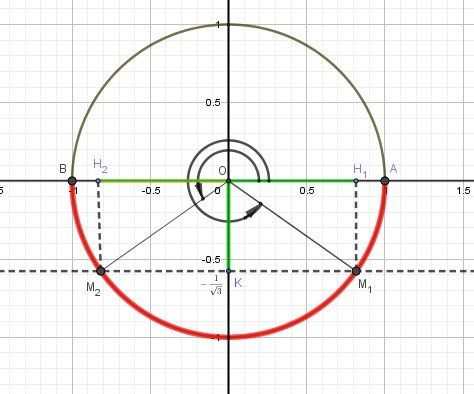
Pour la question 2. Même principe
xxx est une mesure de l'angle (OA→,OM→)(\overrightarrow{OA}, \overrightarrow{OM})(OA,OM)
donc les points M sont forcément sur le demi-cercle rouge.Pour placer les points M :
Sur l'axe des ordonnées, tu places le point K d'ordonnée −13-\dfrac{1}{\sqrt 3} −31 (voisine de −0.577-0.577−0.577)Par K, tu traces la droite perpendiculaire à l'axe des abscisses qui coupe le demi-cercle rouge en M1M_1M1 et M2M_2M2
Les projetés de M1M_1M1 et M2M_2M2 sur l'axe des abscisses sont respectivement H1H_1H1 et H2H_2H2Le cosinus cherchés sont les abscisses de H1H_1H1 et H2H_2H2, c'est à dire OH1‾\overline{OH_1} OH1 et OH2‾\overline{OH_2}OH2 .
Une est positive et l'autre est négative( et elles sont opposées)Par lecture graphique :
cos(x)≈−0.81cos(x)≈-0.81cos(x)≈−0.81 ou cos(x)≈+0.81cos(x)≈+0.81cos(x)≈+0.81
Les calculs permettent d'avoir les valeurs exactes :
cos(x)=−23=−63cos(x)=-\sqrt {\dfrac{2}{3}}=-\dfrac{\sqrt 6}{3}cos(x)=−32=−36 ou cos(x)=+23=+63cos(x)=+\sqrt {\dfrac{2}{3}}=+\dfrac{\sqrt 6}{3}cos(x)=+32=+36
Bonnes constructions.