Intégration par parties

[Franck 29200]

Bonsoir à tous,

Dans le cadre d’un exercice je suis amené à calculer l’intégrale suivante :

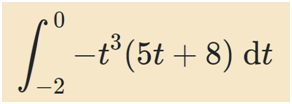
Compte tenu de mes connaissances, j’ai pris le parti d’effectuer une intégration par partie en posant :
U’ = $-t^3$ et V = 5t+8
Ce qui me donne :
U = $(-t^4)/4$ et V’ = 5
Le calcul de [UV] aux bornes -2 à 0 me donne -8

Me reste à calculer l'intégrale suivante afin de retrancher son résultat à -8 et ainsi obtenir le résultat final.

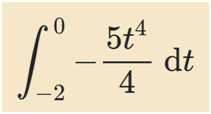
L’ennui c’est que le résultat de cette intégrale est sensé être -8. Résultat affiché par la correction de l’exercice, que j’ai pu confirmer avec l’outil dccode.fr. Le résultat final, quant à lui est : 0 (ce qui confirme le résulta du calcul de [UV] aux bornes de -2 à 0)

Or, pour ma part, je trouve 20. J’ai retourné le calcul (qui ne parait pourtant pas bien sorcier) dans tous les sens sans pour autant parvenir à comprendre comment obtenir -8.

Je vous expose ma méthode afin que vous puissiez débusquer mon erreur.

Quand je calcule $(–5t^4)/4$ pour t = 0 je trouve 0 et quand j’effectue ce même calcul avec t=-2, je trouve 20
J’effectue le calcul dans l’ordre suivant :
$(-2{)}^4$=16
$16\ast 5$=80
$80/4$=20
Ce qui, à cause du signe négatif du numérateur, se transforme en -20, mais se retransforme en +20 lorsque l’on retire la parenthèse.

Je ne vois vraiment pas où est mon erreur.

D'avance, merci.

[Black-Jack]

Bonjour,

Une IPP est inutile. L'intégration est immédiate sans cela.

-t³(5t+8)
= -5t^4 - 8t

Et donc une primitive est : -t^5 - 4t²

Et donc l'intégrale vaut ...

EDIT:

Il fallait bien entendu lire :

-t³(5t+8)
= -5t^4 - 8t³

Et donc une primitive est : -t^5 - 2t^4

Et donc l'intégrale vaut ...

[Franck 29200]

Tellement obnubilé par les intégrations par parties que j'en ai oublié de développer...

[Franck 29200]

En revanche j'obtiens $-5t^4-8t^3$
Avec en primitive $-t^5-2t^4$
Avec un résulta final de 0 (conforme au résultat attendu)

[Franck 29200]

Merci de m'avoir fait penser à développer pour simplifier l'expression. Cela me permet d'avoir un résultat correct à mon exercice.

En revanche, aurais tu une idée du pourquoi je ne parviens pas à obtenir -8 en effectuant ce calcul?

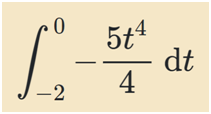
pour mémoire, j'ai effectué les étapes suivantes :
$(-2{)}^4=16$
$16\ast 5=80$
$80/4=20$ pour un résultat attendu de : $-8$

[Noemi]

@Franck-29200 Bonsoir,

Tu fais les calculs sur $f(t)$ donc c'est normal que tu ne trouves pas le résultat.

As tu calculé la primitive ?

[Franck 29200]

Quelle nouille je suis! Je n'ai pas calculé la primitive de UV.

Effectivement en calculant la primitive, qui est : $-t^5/4$ j'obtiens bien -8. Cela me permets d'obtenir le résultat final de mon intégration par partie (inutile ) de 0.

Merci pour vos contributions.

[Noemi]

@Franck-29200

Parfait si tu as pu terminer l'exercice.