Tableaux de signe comment trouver le x ??

Bonjour j’ai un dm et je ne comprend pas comment trouver le x dans l’exercice j’ai bien compris comment il fallait le dresser le tableau ainsi que comment placer les deux signe, je connais la formule pour trouver le x mais je ne comprend à quoi est égale « mx » et « p »
il est écrit dans l’exercice :
On considère deux fonctions affines f et g définies sur R telles que :
.f(5) = 0 et g(3)=0 ;
.f est une fonctions strictement décroissante ;
.f(x)-g(x) = 0 admet pour solution 4
Dresser sur R le tableau de signe de chacune des fonctions f et g
Pouvez m’aider merci ! Bonne journée

@_nxoelia_ , bonjour,

Quelques pistes,

Je te conseille de faire un schéma pour éclairer la question.

Soit $D_f)$ , en rouge, la représentation graphique de $f$
Elle passe par la point $A (5, 0)$ vu que $f (5) = 0$ et $f$ est une fonctions strictement décroissante
Tu en déduis les signes
Pour $x = 5$ , $f (x) = 0$
Pour $\lt 5$ , $\gt 0$
Pour $\gt 5$ , $\lt 0$
Tu fais le tableau de signes usuel

Soit $D_g)$ , en bleu, la représentation graphique de g
Elle passe par la point B(3,0)
Vu que f(x)-g(x) = 0 admet pour solution 4, $f (4) = g (4)$
$D_f)$ et $D_g)$ se coupent en un point D d'abscisse 4
(L'ordonnée de $D$ est forcément strictement positive vu que f est strictement décroissante.
$D_g)$ passe par donc par D et par B. La fonction $g$ est donc strictement croissante.
Tu en déduis les signes
Pour $x = 3$ , $g (x) = 0$
Pour $\lt 3$ , $\lt 0$
Pour $\gt 3$ , $\gt 0$
Tu fais le tableau de signes usuel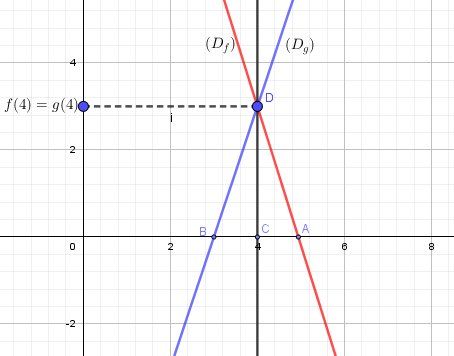

Regarde tout ça de près et reposte si besoin.