Etude d'une fonction avec un logarithme népérien

Bonjour, pouvez vous me dire la domaine de définition de (|lnx|)/x s'il vous plaît
Je suis totalement bloqué

Si j'ai bien lu $f(x)=∣lnx∣xf(x)=\dfrac{|lnx|}{x}$

Conditions :
$x≠0x\ne 0$ pour que le dénominateur soit non nul
$x>0x\gt 0$ pour que lnx existe
pas de condition pour la valeur absolue.

Le domaine de définition de f est dons : $Df=]0,+∞[D_f=]0,+\infty[$

@mtschoon Oui, merci beaucoup, j'ai déjà pensé à cette réponse mais j'étais pas sûr de moi.. j'étudie même cette fonction en ce moment !

C'est très bien @Jese-rajaompandresena , si tout est OK pour toi maintenant.

@mtschoon Pardon Monsieur, pouvez vous me dire la dérivabilité de ce fonction quand x tend vers 0 ? Et comment est le f(0) dans ce cas...

@Jese-rajaompandresena , bonjour,

C'est sans importance, mais ce n'est pas "Monsieur" mais "Madame"., mais le pseudo suffit !

Ta question est très bizarre si la fonction f est bien celle que tu as donné :
$f(x)=∣lnx∣xf(x)=\dfrac{|lnx|}{x}$

Comme déjà indiqué, lnx n'existe que pour $x>0x\gt 0$ , c'est pour cela que le domaine de f est $]0,+∞[\boxed{]0,+\infty[}$

Donc : $f (0)$ n'existe pas.
f n'est pas définie en 0, donc pas dérivable en 0.

Lorsque x tend vers 0 par valeurs positives, tu peux prouver que $f (x)$ tend vers $+∞+\infty$
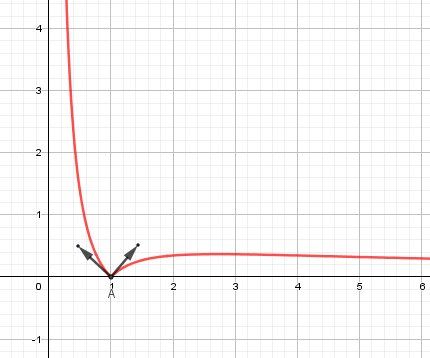
La représentation graphique a une asymptote "verticale" d'équation $x = 0$

@mtschoon Oh, je suis vraiment désolé Madame
Enfaite, sur le sujet, il demande la dérivabilité en tout point de Df.. alors, dois-je aussi faire la dérivabilité en plus Infini ?

@Jese-rajaompandresena ,

Non, le domaine va de 0 (non pris), jusqu'à $+∞+\infty$ (non pris).

Tu étudies la dérivée pour tout réel x strictement positif.

@mtschoon Merci beaucoup, je comprends très bien.. Merci encore pour votre aide, vous me sauvez !!
Mais êtes-vous prof?

@Jese-rajaompandresena ,

Réponse : prof à la retraite .

(Lorsque j'étais prof en activité, je m'occupais beaucoup de mes élèves et je n'avais pas le temps d'aider sur un forum...)

@mtschoon Je vois.. Mais je vous dois du respect Madame!! Moi je suis encore lycéens en classe de TC

@Jese-rajaompandresena ,

C'est très bien d'être en TC !

Pour la dérivabilité pour $x>0x\gt 0$ , j'espère que tu n'auras pas de problème.

A cause de la valeur absolue, tu dois faire 3 cas .

ler cas : $x>1x\gt 1$ donc $lnx>0lnx\gt 0$ donc $f(x)=lnxxf(x)=\dfrac{lnx}{x}$

Tu utilises les formules usuelles pour calculer $f^{'} (x)$

2ème cas : $0<x<10\lt x\lt 1$ donc $lnx<0lnx\lt 0$ donc $f(x)=−lnxxf(x)=\dfrac{-lnx}{x}$

Tu utilises les formules usuelles pour calculer $f^{'} (x)$

3ème cas : $x = 1$
Il faut étudier séparément la dérivabilité à gauche et la dérivabilité à droite (en passant par la définition).
Si tu obtiens un nombre dérivé à gauche différent d'un nombre dérivé à droite, il faudra conclure que f n'est pas dérivable pour x=1.

Tu peux donner tes réponses si tu as besoin d'une vérification.

Bons calculs.

@mtschoon Wow, je suis déjà sur la bonne voie merci!! Mais Pourquoi la troisième cas existe madame ?

@Jese-rajaompandresena , bonjour,

Je te réponds à ta question relative au 3ème cas, c'est à dire pour $x = 1$ "frontière" entre les deux premiers cas indiqués.

Rappelle toi la définition de base pour une fonction dérivable pour une valeur x

$lim⁡h→0f(x+h)−f(x)h=f′(x)\displaystyle \lim_{h\to 0}\dfrac{f(x+h)-f(x)}{h}=f'(x)$

$h→0h\to 0$ veut dire que $h$ tend vers $0$ , aussi bien par valeurs positives(c'est à dire supérieures à 0) que par valeurs négatives (c'est à dire inférieures à 0)

Pour le cas $x = 1$
il faut étudier :
$lim⁡h→0f(1+h)−f(1)h\displaystyle \lim_{h\to 0}\dfrac{f(1+h)-f(1)}{h}$

Suivant que $h$ est supérieur ou inférieur à $0$ , $1 + h$ est supérieur ou inférieur à $1$ et $f (1 + h)$ change d'xpression .

Il faut donc faire deux études : une à droite de 1 et une à gauche de 1

Dérivabilité à droite de 1 :
$lim⁡h→0+f(1+h)−f(1)h=a1\displaystyle \lim_{h\to 0^+}\dfrac{f(1+h)-f(1)}{h}=a_1$
le nombre $a_1$ (lorsqu'il existe) est le nombre dérivée à droite.
et on dit que la fonction f est dérivable, en 1, à droite.
$a_1$ est le coeficient directeur de la demi tangente à la représentation graphique pour $x = 1$ à droite.

Dérivabilité à gauche de 1 :
$lim⁡h→0−f(1+h)−f(1)h=a2\displaystyle \lim_{h\to 0^-}\dfrac{f(1+h)-f(1)}{h}=a_2$
le nombre $a_2$ (lorsqu'il existe) est le nombre dérivée à gauche.
et on dit que la fonction f est dérivable, en 1, à gauche.
$a_2$ est le coeficient directeur de la demi tangente à la représentation graphique pour $x = 1$ à gauche

Lorsque $a1≠a2a_1\ne a_2$ , on dit que la fonction f n'est pas dérivable en 1.
La représentation graphique n'a pas une tangente pour $x = 1$ vu que les deux demi_tangentes ne forment pas une droite.

Bonne lecture.

Si tu le souhaites, tu peux donner tes réponses pour vérification.

@mtschoon J'ai trouvé que a1 est égale à a2
Est-ce correct ?

@Jese-rajaompandresena ,

Ce serait bien d'indiquer tes calculs, ou bien de les revoir.

Sauf erreur, tu aurais dû trouver : $a_1=1$ et $a_2=-1$

@Jese-rajaompandresena , je t'indique un calcul pour trouver $a_1$ , si besoin.

Dérivabilité à droite de 1

On cherche
$lim⁡h→0+f(1+h)−f(1)h\displaystyle \lim_{h\to 0^+} \dfrac{f(1+h)-f(1)}{h}$

$f (1) = 0$
vu que $1+h>11+h\gt 1$ , $f(1+h)=ln(1+h)1+hf(1+h)=\dfrac{ln(1+h)}{1+h}$

$lim⁡h→0+f(1+h)−f(1)h=ln(1+h)1+hh=ln(1+h)h(1+h)\displaystyle \lim_{h\to 0^+} \dfrac{f(1+h)-f(1)}{h}=\dfrac{\dfrac{ln(1+h)}{1+h}}{h}=\dfrac{ln(1+h)}{h(1+h)}$

Pour lever l'indétermination de la forme $00\dfrac{0}{0}$ on décompose :

$lim⁡h→0+f(1+h)−f(1)h=ln(1+h)h×11+h\displaystyle \lim_{h\to 0^+} \dfrac{f(1+h)-f(1)}{h}=\dfrac{ln(1+h)}{h}\times \dfrac{1}{1+h}$

On sait que (limite usuelle-voir cours) $lim⁡x→0ln(1+x)x=1\displaystyle \lim_{x\to 0} \dfrac{ln(1+x)}{x}=1$ , donc
$lim⁡h→0+ln(1+h)h=1\displaystyle \lim_{h\to 0^+} \dfrac{ln(1+h)}{h}=1$
De plus :
$lim⁡h→0+11+h=1\displaystyle \lim_{h\to 0^+} \dfrac{1}{1+h}=1$

Conclusion :

$lim⁡h→0+f(1+h)−f(1)h=1×1=1\displaystyle \lim_{h\to 0^+} \dfrac{f(1+h)-f(1)}{h}=1\times 1=1$

$a1=1\boxed{a_1=1}$

Pour la dérivabilité à gauche en 1, tu appliques le même raisonnement, mais dans ce cas, vu que $1+h<11+h\lt 1$ , $f(1+h)=−ln(1+h)1+hf(1+h)=-\dfrac{ln(1+h)}{1+h}$
Tu trouves ainsi :
$a2=−1\boxed{a_2=-1}$

Regarde tout ça de près et tu pourras déduire que l'ensemble de dérivabilité de f est $]0,1[∪]1,+∞[]0,1[\cup ]1,+\infty[$

Bonjour,

Pistes pour la fin , pour consultation éventuelle (@Jese-rajaompandresena a dû déjà terminer son exercice)

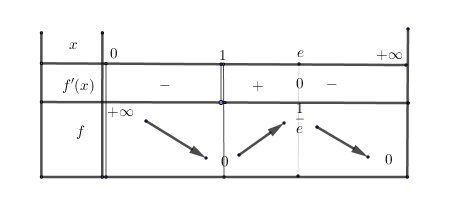
Pour $0<x<10\lt x\lt 1$ : $f(x)=−lnxxf(x)=\dfrac{-lnx}{x}$ d'où $f′(x)=−1+lnxx2f'(x)=\dfrac{-1+lnx}{x^2}$ , $f′(x)<0f'(x)\lt 0$

Pour $x>1x\gt 1$ : $f(x)=lnxxf(x)=\dfrac{lnx}{x}$ d'où $f′(x)=1−lnxx2f'(x)=\dfrac{1-lnx}{x^2}$
Pour $1<x<e1\lt x\lt e$ , $f′(x)>0f'(x)\gt 0$
Pour $x = e$ , $f^{'} (x) = 0$
Pour $x>ex\gt e$ , $f′(x)<0f'(x)\lt 0$

Bonne lecture éventuelle.