Partie calcul littéral d'un exercice de dérivation

Bonjour cela fait plusieurs jour que je cherche à résoudre cet exercice sans pouvoir y parvenir voici l'énoncé :
Soit a et b deux réels. On admet que la fonction f est définie par f(x)= 2(x^2+ax+b)/x^2+2x+5

1.montrer que pour tout x €R
x^2+2x+5=(x+1)^2+4 et justifier alors l'ensemble de définition de f.
2. On sait que la courbe C passe par le point A(0;2/5) montrer que b=1
3. Démontrer que pour tout x €R, f'(x)=(4-2a)x^2+16x+10a-4/(x^2+2x+5)^2
4. On sait que la courbe C admet au point d'abscisse-3 une tangente horizontale. Démontrer que a=-2
5.demontrer que, pour tout x € R, f'(x)=8(x+3)(x-1)/(x^2+2x+5)^2
6. En déduire alors le signe de f'(x) puis dresser le tableau de variations de la fonction f.

@ada , bonjour,

Je regarde ton énoncé,

@ada a dit dans Partie calcul littéral d'un exercice de dérivation :

Soit a et b deux réels. On admet que la fonction f est définie par f(x)= 2(x^2+ax+b)/x^2+2x+5

1.montrer que pour tout x €R
x^2+2x+5=(x+1)^2+4 et justifier alors l'ensemble de définition de f.
2. On sait que la courbe C passe par le point A(0;2/5) montrer que b=1
3. Démontrer que pour tout x €R, f'(x)=(4-2a)x^2+16x+10a-4/(x^2+2x+5)^2
4. On sait que la courbe C admet au point d'abscisse-3 une tangente horizontale. Démontrer que a=-2
5.demontrer que, pour tout x € R, f'(x)=8(x+3)(x-1)/(x^2+2x+5)^2
6. En déduire alors le signe de f'(x) puis dresser le tableau de variations de la fonction f.

Je pense que tu as voulu écrire : $f(x)=2(x2+ax+b)x2+2x+5f(x)=\dfrac{2(x^2+ax+b)}{x^2+2x+5}$

Vu que tu n'utilises pas le Latex, il aurait fallu mettre des parenthèses autour de $x^2+2x+5$ pour que l'on comprenne qu'il s'agit du dénominateur.

Quelques pistes pour démarrer,

Pour le 1) tu as le choix.

Tu peux te contenter de développer le membre de droite avec l'identité remarquable usuelle et après simplifacation, tu trouves le membre de gauche.

Autre façon (la meilleure, je trouve) : tu pars du membre de gauche et tu le décomposes.
$x^2+2x+5=(x^2+2x+1)+4$
En reconnaissant l'identité remarquable $x^2+2x+1=(x+1)^2$ tu obtiens directement:
$x^2+2x+5=(x+1)^2+4$

Conséquence :
Pour tout $x$ réel, $(x+1)2≥0(x+1)^2 \ge 0$

En ajoutant 4 : $(x+1)2+4>0(x+1)^2 +4\gt 0$ donc le dénominateur de $f (x)$ est strictement positif, donc ne s'annule pas donc :
$Df=R\boxed{D_f=R}$

@ada , Piste pour le 2)

$f(0)=25f(0)=\dfrac{2}{5}$

Dans l'expression de $f (x)$ tu remplaces $x$ par 0, ce qui te donne :
$2b5=25\dfrac{2b}{5}=\dfrac{2}{5}$
Tu en déduis la valeur de $b$

Essaie de poursuivre et donne des réponses pour aide/vérification si tu as besoin.

@ada , Piste pour le 3)

Tu as donc maintenant $f(x)=2(x2+ax+1)x2+2x+5f(x)=\dfrac{2(x^2+ax+1)}{x^2+2x+5}$

Tu dérives en utilisant la dérivée d'un quotient (voir cours) et tu obtiendras le résultat donné dans ton énoncé.

@ada , Piste pour le 4)

Tu dois utiliser $f^{'} (- 3) = 0$ pour trouver $a$

Reposte si besoin.

@mtschoon merci pour votre aide ! Je reprend mes recherches et je vous retiendrais au courant en cas de soucis

D'accord @ada .
Reposte si tu bloques.

COMPLEMENT éventuel

Piste de Calcul du 3)

$f(x)=2(x2+ax+1)x2+2x+5f(x)=\dfrac{2(x^2+ax+1)}{x^2+2x+5}$

$U(x)=2(x^2+ax+1)$
$U^{'} (x) = 2 (2 x + a)$
$V(x)=x^2+2x+5$
$V^{'} (x) = 2 x + 2$
$f′(x)=U′(x)V(x)−U(x)V′(x)(V(x))2f'(x)=\dfrac{U'(x)V(x)-U(x)V'(x)}{(V(x))^2}$

Après calcul :
$f′(x)=(4−2a)x2+18x+10a+2(x2+2x+5)2\boxed{f'(x)=\dfrac{(4-2a)x^2+18x+10a+2}{(x^2+2x+5)^2}}$

Conséquence ( le 4 ):
$f^{'} (x) = 0$ <=> $4-2a)x^2+18x+10a+2=0$

Donc :

$f^{'} (- 3) = 0$ <=> $9 (4 - 2 a) - 54 + 10 a + 2 = 0$

Après caclul, on obtiens $a = - 2$ comme indiqué dans l'énoncé

D'où :

$f(x)=2(x2−2x+1)x2+2x+5\boxed{f(x)=\dfrac{2(x^2-2x+1)}{x^2+2x+5}}$

Pour vérification éventuelle,

Tableau de signes permettant d'avoir le signe de la dérivée :

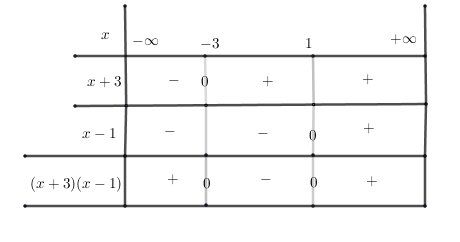
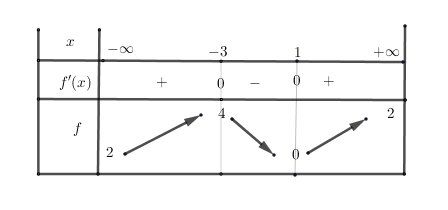
Tableau de variations de f (les limites en $+∞+\infty$ et $−∞-\infty$ ne sont à mettre que si le principe de l'étude a été vu en cours)