Système d'équation carré et cube

bonsoir
désolé pour la longue absence quelques soucis!
j'ai ce système qui me fait réfléchir!

soit $(x, y)$ appartenant à $R$ vérifiant le système $x^2 + y^2=2$ , $x^3 + y^3=2$
déterminer les valeur de $x + y$
perso j'ai essaye combinaison et substitution je bute j'ai aussi essayé changement de variable sans succès!

@loicstephan , bonjour,
Je regarde ta question :
@loicstephan a dit dans Système d'équation carré et cube :

soit $(x, y)$ appartenant à $R$ vérifiant le système $x^2 + y^2=2$ , $x^3 + y^3=2$
déterminer les valeur de $x + y$

Une piste possible : arriver à une équation du 3ème degré en (x+y), simple à résoudre.
(ce n'est qu'une piste, tu dois faire les calculs)

$x^3+y^3=2$ <=> $x+y)(x^2-xy+y^2)=2$

En remplaçant $x^2+y^2$ par $2$ , tu obtiens :
$(x + y) (2 - x y) = 2$ (formule 1)

$x^2+y^2=2$ <=> $x+y)^2-2xy=2$ (formule 2)

Dans cette formule 2, tu peux exprimer $x y$ en fonction de $(x + y)$ :
$xy=12(x+y)2−1xy=\dfrac{1}{2}(x+y)^2-1$

En substituant dans la formule 1, tu obtiens :
$(x+y)(2−12(x+y)2−1)=2(x+y)\biggr(2-\dfrac{1}{2}(x+y)^2-1\biggr)=2$

Pour alléger, tu peux poser $X = x + y$

Tu obtiens ainsi l'équation $−12X3+3X−2=0\boxed{-\dfrac{1}{2}X^3+3X-2=0}$

Solution évidente : $X = 2$
Tu mets $(X - 2)$ en facteur.
Le second facteur est du second degré et tu dois trouver, sauf erreur, après résolution : $X=−1−3X=-1-\sqrt 3$ et $X=−1+3X=-1+\sqrt 3$

Conclusion :
trois valeurs possibles pour $x + y$ : $2,−1−3,−1+3\boxed{2,-1-\sqrt 3, -1+\sqrt 3}$

Recompte car j'ai fait vite.

Bonjour,

Juste pour le fun ... On peut trouver les couples (x,y) qui conviennent.
Mais en le faisant, sauf erreur de ma part, on trouve qu'une des solutions données par mtschoon pour (x+y) ne convient pas.

x²+y² = 2
x³+y³ = 2

x²+y²=2 impose |x| <= sqrt(2) et |y| <= sqrt(2)

y = +/- sqrt(2-x²)

y³ = +/- (2-x²)*sqrt(2-x²)

et donc +/- (2-x²)*sqrt(2-x²) + x³ = 2

x = +/- sqrt(2) n'est pas solution et donc :

+/- sqrt(2-x²) = (2-x³)/(2-x²)

en élevant au carré (risque d'engendrer des solutions parasites ... et donc il faudra vérifier si les solutions trouvées conviennent ou non ...)

(2-x²)³ = (2-x³)²

8 + 6x^4 - 12x² - x^6 = 4 + x^6 - 4x³

2.x^6 - 6x^4 - 4x³ + 12x² - 4 = 0

x^6 - 3x^4 - 2x³ + 6x² - 2 = 0

x = 1 et une solution "dite" évidente --> x^6 - 3x^4 - 2x³ + 6x² - 2 est divisible par (x-1)

x^6 - 3x^4 - 2x³ + 6x² - 2 = (x-1)(x^5 + x^4 - 2x³ - 4x² + 2x + 2)

Et x = 1 est encore solution "évidente" de (x^5 + x^4 - 2x³ - 4x² + 2x + 2) = 0 --> (x^5 + x^4 - 2x³ - 4x² + 2x + 2) est divisible par (x-1)

On trouve : x^6 - 3x^4 - 2x³ + 6x² - 2 = (x-1)².(x^4 + 2x³-4x-2)

Reste à trouver les solutions de x^4 + 2x³-4x-2 = 0

Les solutions réelles sont (Ferraris) x = 1/2*(-1 - sqrt(2) * 3^(1/4) + sqrt(3))
et x = 1/2*(-1 + sqrt(2) * 3^(1/4) + sqrt(3))

On a donc comme valeurs réelles possibles de x (dont il faut vérifier si elles conviennent) :

x = 1
x = 1/2*(-1 - sqrt(2) * 3^(1/4) + sqrt(3))
x = 1/2*(-1 + sqrt(2) * 3^(1/4) + sqrt(3))

Et on calcule les valeurs de y correspondante par y = +/- sqrt(2 - x²)

x = 1 ---> y = +/- 1
x = 1/2*(-1 - sqrt(2) * 3^(1/4) + sqrt(3)) = -0,564579... --> y = +/- 1,296630...
x = 1/2*(-1 + sqrt(2) * 3^(1/4) + sqrt(3)) = 1,296630... --> y = +/- 0,564579

En vérifiant toutes ces possibilités avec l'équation x³+y³=2, on ne retient que les couples (x,y) qui conviennent, qui sont :

(1,1) ; ( -0,564579... , 1,296630...) ; (1,296630... , -0,564579...)

Ou si on préfère en valeurs exactes :

(1,1) ; ( 1/2*(-1 - sqrt(2) * 3^(1/4) + sqrt(3)) , 1/2*(-1 + sqrt(2) * 3^(1/4) + sqrt(3))) ; (1/2*(-1 + sqrt(2) * 3^(1/4) + sqrt(3)) , 1/2*(-1 - sqrt(2) * 3^(1/4) + sqrt(3)))

et on peut en déduire les valeurs de (x + y) qui conviennent, soit : 2 et (-1 + sqrt(3))

... Pareil que ce que trouve mtschoon, sauf que (x+y) = -1 - sqrt(3) semble ne pas convenir.

x+y = -1-sqrt(3) est-il OK ?

Si oui, on aurait (x+y)² = (x²+y²+2xy) = (-1 - V3)²
(x²+y²+2xy) = 1 + 3 + 2V3 = 4 + 2V3
mais on sait que x²+y² = 2 -->

2xy = 2 + 2V3
xy = 1 + V3
|xy| = 1 + V3

mais on doit avoir |x| et |y| <= V2 (pour respecter (x²+y²) = 2)
et donc |xy| <= 2 ... ce qui n'est pas respecté avec |xy| = 1 + V3

Sauf erreur de ma part, les seules possibilités (avec x et y réels) sont (x+y) = 2 ou (-1 + sqrt(3))

A vérifier ... bien entendu.

Bonjour,

Je viens passer en revue les valeurs de la somme $x + y$ , obtenue directement.

Evidemment, l’énoncé ne voulait pas faire calculer x et y d’abord, sinon il aurait indiqué « résoudre le système d’inconnue (x,y) », et le calcul de la somme n'aurait plus d'intérêt.

Pour trouver directement la somme, l’élimination du produit $x y$ entre les deux équations est efficace mais il ouvre la porte à une somme supplémentaire « parasite » (on raisonne par implications et non par équivalence)

Plutôt que de vérifier par calcul, j’ai utilisé Geogebra (c'est moins fatigant...)

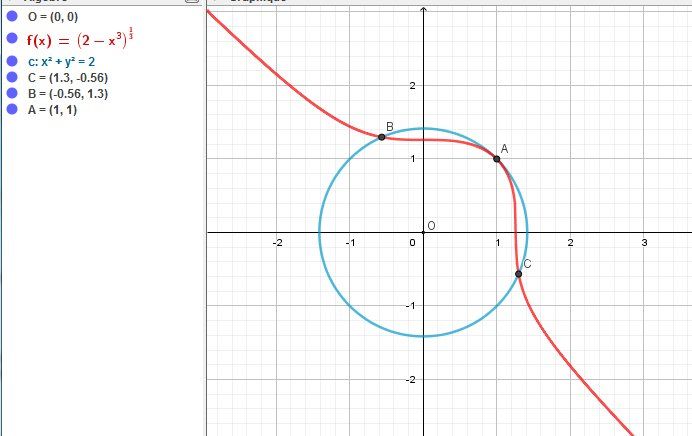
Le solutions (x,y) du système sont les couples de coordonnées des points $A, B, C$ .
La point $A$ correspond à la somme $x + y = 2$
Les points $B$ et $C$ ont des coordonnées "alternées".
Vu les valeurs approchées indiquées, ils correspondent à la somme $x+y=−1+3x+y=-1+\sqrt 3$

Pour la somme, $2$ et $−1+3-1+\sqrt 3$ sont à conserver (et $−1−3-1-\sqrt 3$ est la "réponse parasite")

@mtschoon
Bonjour!
apres factoris

@mtschoon
bonjour
MERCI BCP

De rien @loicstephan et surtout Bon travail !

Merci aussi pour les remerciements exclusifs.

@Black-Jack désole en réalité je m'adressais a tous je ne me suis pas rendu compte que j'étais en réponse seule a @mtschoon