Etude d'une fonction logarithme dépendant d'un paramètre
-
Ffadil gnali dernière édition par
Bonjour à tous j'espère que vous allez bien!
Je recherche une exercice dans lequelle il s'agit d'une étude de cette fonction
f_{n}(x) = (x - 1) ^ n * ln(x) merci d'avance
-
BBlack-Jack dernière édition par
Bonjour,
fn(x) = (x - 1)^n * ln(x)
Dfn : x > 0
fn'(x) = n*(x-1)^(n-1) * ln(x) + (x-1)^n/x
fn'(x) = (x-1)^(n-1) * (n * ln(x) + (x-1)/x)Si n est impair :
(x-1)^(n-1) >= 0 car (n-1) est pair)
fn'(x) = 0 pour x = 1
fn'(x) a le signe de g(x) = (n * ln(x) + (x-1)/x)(n * ln(x) + (x-1)/x) = n * ln(x) + 1 - 1/x
g(x) = n * ln(x) + 1 - 1/x
g'(x) = n/x + 1/x² > 0 et donc g(x) est croissante.
g(1) = 0
et donc g(x) < 0 pour x dans ]0 ; 1[
g(x) = 0 pour x = 1
g(x) > 0 pour x > 1
-->
fn'(x) < 0 pour x dans ]0 ; 1[ --> fn est décroissante.
fn'(x) = 0 pour x = 1
fn'(x) > 0 pour x > 1--> fn est croissante.fn(x) a un minimum en x = 1, ce min vaut fn(1) = 0
Donc fn(x) > 0 sur R/{1} et fn(1) = 0
Si n est pair.
(x-1)^(n-1) < 0 pour x dans ]0 ; 1[
(x-1)^(n-1) = 0 pour x = 1
(x-1)^(n-1) > 0 pour x > 1fn'(x) a le signe contraire de g(x) pour x dans ]0 ; 1[
fn'(x) = 0 pour x = 1
fn'(x) a le signe de g(x) pour x > 1et donc :
fn'(x) > 0 pour x dans ]0 ; 1[ --> fn est croissante.
fn'(x) = 0 pour x = 1
fn'(x) > 0 pour x > 1--> fn est croissante.fn est donc stritement croissante
et on a fn(1) = 0donc fn(x) < 0 pour x dans ]0 ; 1[
fn(x) = 0 pour x = 1
fn(x) > 0 pour x > 1Si c'est au programme ... on peut encore étudier le signe de fn''(x) dans le cas de n pair pour la recherche d'un point d'inflexion.
Je n'ai rien vérifié, à toi de le faire après avoir compris ... et corriger si c'est nécessaire.
-
mtschoon dernière édition par

Bonjour,
@fadil-gnali , il serait heureux de préciser à quel ensemble de nombres appartient nnn.
Est-ce NNN ? ou bien N∗?N^* ?N∗? ou bien ZZZ ? ou bien ...???
-
Ffadil gnali dernière édition par
@mtschoon N*
-
Ffadil gnali dernière édition par
@Black-Jack d'accord merci je me mets au travail
-
mtschoon dernière édition par

Merci @fadil-gnali d'avoir complété l'indication sur nnn : naturel non nuL.
Ton énoncé est complet maintenant.
Travaille bien.
-
mtschoon dernière édition par

Bonjour,
@fadil-gnali a dû finir son travail.
Seulement une synthèse pour consultation éventuelle.
Pour nnn naturel pair non nul :
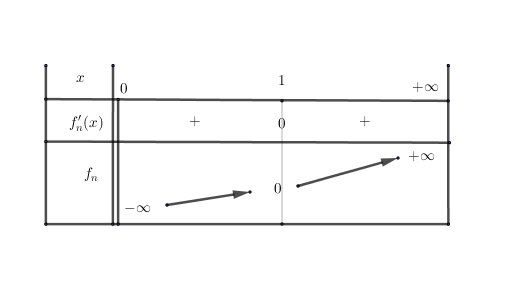
Illustration graphique :
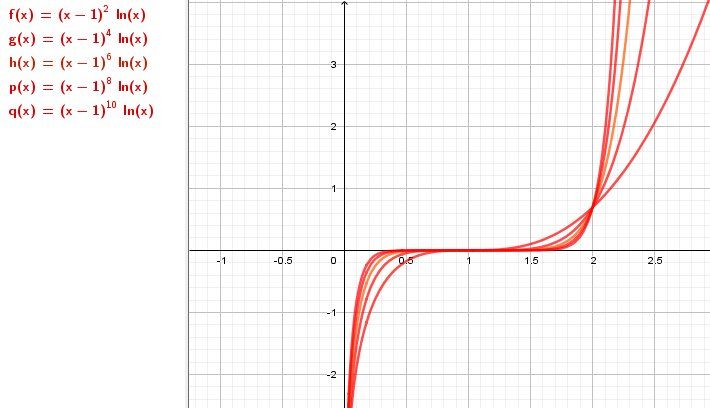
-
mtschoon dernière édition par

Pour nnn naturel impair :
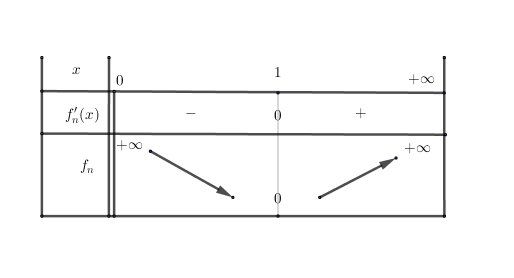
Illustration graphique
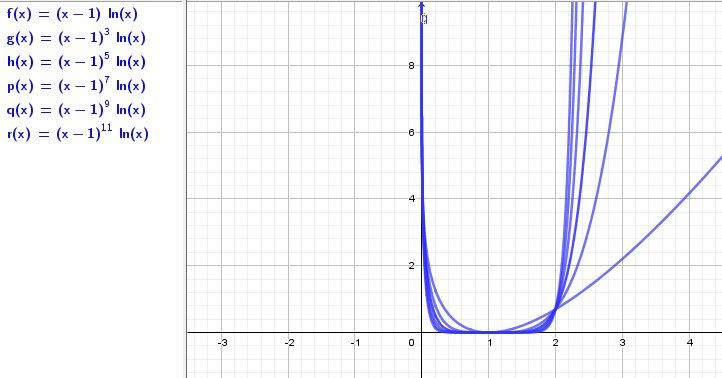
Bonne consultation éventuelle.
-
Ffadil gnali dernière édition par
@mtschoon bonsoir merci beaucoup pour les précisions sur la courbe
-
mtschoon dernière édition par

De rien @fadil-gnali .
C'est parfait si ça t'a éclairé.