Exercice produit scalaire

Bonjour à tous j'ai un exercice de produit scalaire que je n'arrive pas à traiter
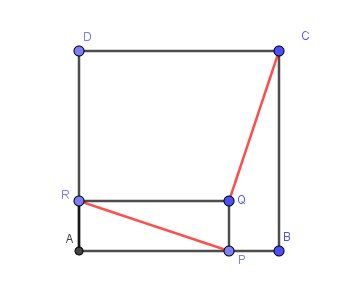
Soit un carré ABCD. On construit un rectangle APQR tel que :

P et R sont sur les côtés [AB] et [AD] du carré ;
AP = DR.Le problème a pour objet de montrer que les droites (CQ) et (PR) sont perpendiculaires.

Justifier que : CQ.PR=CQ.(AR-AP)
En déduire que les droites (CQ) et (PR) sont perpendiculaires
J'ai réussi à faire la première question mais la deuxième là je trouve pas si vous pouvez m'aider merci d'avance

@serme225 , bonjour,

Je joins un schéma pour plus de clarté,

@serme225 , vu que tu as fait la première question, en utilisant la relation de Chasles, tu as trouvé:

$CQ→.PR→=CQ→.(AR→−AP→)\overrightarrow{CQ}.\overrightarrow{PR}=\overrightarrow{CQ}.(\overrightarrow{AR}-\overrightarrow{AP})$

Piste pour la seconde question,

En développant la relation de la question 1):
$CQ→.PR→=CQ→.AR→−CQ→.AP→\overrightarrow{CQ}.\overrightarrow{PR}=\overrightarrow{CQ}.\overrightarrow{AR}-\overrightarrow{CQ}.\overrightarrow{AP}$

Tu calcules séparémment ces deux produits scalaires avec le théorème de la projection (voir cours)

En projetant sur (AD) :
$CQ→.AR→=DR→.AR→\overrightarrow{CQ}.\overrightarrow{AR}=\overrightarrow{DR}.\overrightarrow{AR}$
Ces vecteurs étant de sens contraire :
$CQ→.AP→=−DR×AR\overrightarrow{CQ}.\overrightarrow{AP}=-DR\times AR$

En projetant sur (AB) :
$CQ→.AP→=BP→.AP→\overrightarrow{CQ}.\overrightarrow{AP}=\overrightarrow{BP}.\overrightarrow{AP}$
Ces vecteurs étant de sens contraire :
$CQ→.AP→=−BP×AP\overrightarrow{CQ}.\overrightarrow{AP}=-BP\times AP$

D'où :
$CQ→.PR→=(−DR×AR)+(BP×AP)\overrightarrow{CQ}.\overrightarrow{PR}=(-DR\times AR)+(BP\times AP)$

Tu poursuis en calculant cette valeur et tu dois trouver 0

DONC :
$CQ→.PR→=0\boxed{\overrightarrow{CQ}.\overrightarrow{PR}=0}$ et tu tires la conclusion.