mathématiques 1ère générale
-
hugo.mt_22 dernière édition par
Dans le plan muni d'un repère orthonormé, soient les points A(5;-7) et B(−4;8).
Donner une équation de la médiatrice du segment [AB].
-
mtschoon dernière édition par

@hugo-mt_22 , bonjour,
As-tu , dans ton cours, la formule de distance entre deux points ?
Si c'est le cas :
Tout point M(x,y)M(x,y)M(x,y) de la médiatrice de [AB] satisfait à MA=MBMA=MBMA=MB(x−xA)2+(y−yA)2=(x−xB)2+(y−yB)2\sqrt {(x-x_A)^2+(y-y_A)^2}=\sqrt {(x-x_B)^2+(y-y_B)^2}(x−xA)2+(y−yA)2=(x−xB)2+(y−yB)2
En élevant au carré ( pour supprimer les radicaux) et en calculant/simplifiant, tu obtiendras l'équation cherchée.
Sinon, il faudra passer par le point I milieu de [AB] et le produit scalaire AB→.IM→=0\overrightarrow{AB}.\overrightarrow{IM}=0AB.IM=0, par exemple.
Tu peux donner ta réponse pour vérification si tu le souhaites.
-
hugo.mt_22 dernière édition par
@mtschoon cela fait racine carrée de x^2+8x+80+y^2-16y et racine carrée de x^2-10x+74+y^2+14y
-
mtschoon dernière édition par mtschoon

Continue.
Après développements, transpositions, simplifications, il doit rester, sauf erreur,
−18x+30y−6=0-18x+30y-6=0−18x+30y−6=0
En divisant par 6
−3x+5y−1=0-3x+5y-1=0−3x+5y−1=0
Tu peux mettre sous la forme :
y=35x+15y=\dfrac{3}{5}x+\dfrac{1}{5}y=53x+51Pour vérifier, tu peux faire l'autre méthode pour voir si on trouve pareil
-
mtschoon dernière édition par mtschoon

Illustration graphique:
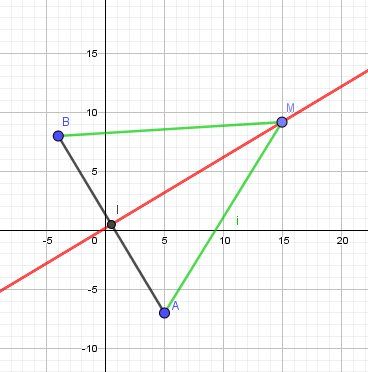
-
hugo.mt_22 dernière édition par
@mtschoon bonjour si je trouve cela comment simplifier, transposer etc...
racine carrée x^2-4x+29+y^2+10y et racine carrée x^2+12x+45+y^2+6yMerci
-
mtschoon dernière édition par mtschoon

@hugo-mt_22 , bonjour,
Je veux bien détailler si tu le souhaites, mais faire tous les calculs à ta place ne te fera pas faire de progrès...
Il faut trouver un juste milieu et ce n'est pas facile !Je pars de ce que tu avais trouvé :
@hugo-mt_22 a dit dans mathématiques 1ère générale :
@mtschoon cela fait racine carrée de x^2+8x+80+y^2-16y et racine carrée de x^2-10x+74+y^2+14y
x2+8x+80+y2−16y=x2−10x+74+y2+14y\sqrt{ x^2+8x+80+y^2-16y }=\sqrt{x^2-10x+74+y^2+14y}x2+8x+80+y2−16y=x2−10x+74+y2+14y
Tu supprimes les radicaux (c'est à dire tu élèves au carré) ;
x2+8x+80+y2−16y=x2−10x+74+y2+14yx^2+8x+80+y^2-16y =x^2-10x+74+y^2+14y x2+8x+80+y2−16y=x2−10x+74+y2+14yTu simplifies x2x^2x2 avec x2x^2x2 et y2y^2y2 avec y2y^2y2 (en bref, tu les barres ) et il reste
8x+80−16y=−10x+74+14y8x+80-16y=-10x+74+14y8x+80−16y=−10x+74+14yTu transposes dans le membre de gauche (en changeant les signes des termes transposés) et tu obtiens
8x+80−16y+10x−74−14y=08x+80-16y+10x-74-14y=08x+80−16y+10x−74−14y=0
c'est à dire :
(8x+10x)+(−16y−14y)+(80−74)=0(8x+10x)+(-16y-14y)+(80-74)=0(8x+10x)+(−16y−14y)+(80−74)=0
c'est à dire
18x−30y+6=018x-30y+6=018x−30y+6=0
en divisant par 6
3x−5y+1=0\boxed{3x-5y+1=0}3x−5y+1=0
si tu préfères, tu peux multiplier par -1 : −3x+5y−1=0\boxed {-3x+5y-1=0}−3x+5y−1=0si tu souhaites avoir l'équation sous la forme y=ax+by=ax+by=ax+b , tu isoles 5y5y5y puis yyy
5y=3x+15y=3x+15y=3x+1 d'où, en divisant par 3 :
y=35x+15\boxed{y=\dfrac{3}{5}x+\dfrac{1}{5}}y=53x+51Refais seul ces calculs.
Bon travail .
-
hugo.mt_22 dernière édition par
@mtschoon cela ferais pour le calcul que j'ai mis avant votre détail -16x-16+4y=0
-
mtschoon dernière édition par mtschoon

@hugo-mt_22 , non ta dernière proposition n'est pas bonne.
Relis le calcul que je t'ai donné.
-
hugo.mt_22 dernière édition par
@mtschoon comment faire ?
-
mtschoon dernière édition par mtschoon

Désolée @hugo-mt_22 mais je ne sais pas de quoi tu parles.
@hugo-mt_22 a dit dans mathématiques 1ère générale :
@mtschoon cela fait racine carrée de x^2+8x+80+y^2-16y et racine carrée de x^2-10x+74+y^2+14y
J'ai fait tout le calcul en partant de cette égalité exacte que tu as trouvée, ici
@mtschoon a dit dans mathématiques 1ère générale :
@hugo-mt_22 , bonjour,
Je veux bien détailler si tu le souhaites, mais faire tous les calculs à ta place ne te fera pas faire de progrès...
Il faut trouver un juste milieu et ce n'est pas facile !Je pars de ce que tu avais trouvé :
@hugo-mt_22 a dit dans mathématiques 1ère générale :
@mtschoon cela fait racine carrée de x^2+8x+80+y^2-16y et racine carrée de x^2-10x+74+y^2+14y
x2+8x+80+y2−16y=x2−10x+74+y2+14y\sqrt{ x^2+8x+80+y^2-16y }=\sqrt{x^2-10x+74+y^2+14y}x2+8x+80+y2−16y=x2−10x+74+y2+14y
Tu supprimes les radicaux (c'est à dire tu élèves au carré) ;
x2+8x+80+y2−16y=x2−10x+74+y2+14yx^2+8x+80+y^2-16y =x^2-10x+74+y^2+14y x2+8x+80+y2−16y=x2−10x+74+y2+14yTu simplifies x2x^2x2 avec x2x^2x2 et y2y^2y2 avec y2y^2y2 (en bref, tu les barres ) et il reste
8x+80−16y=−10x+74+14y8x+80-16y=-10x+74+14y8x+80−16y=−10x+74+14yTu transposes dans le membre de gauche (en changeant les signes des termes transposés) et tu obtiens
8x+80−16y+10x−74−14y=08x+80-16y+10x-74-14y=08x+80−16y+10x−74−14y=0
c'est à dire :
(8x+10x)+(−16y−14y)+(80−74)=0(8x+10x)+(-16y-14y)+(80-74)=0(8x+10x)+(−16y−14y)+(80−74)=0
c'est à dire
18x−30y+6=018x-30y+6=018x−30y+6=0
en divisant par 6
3x−5y+1=0\boxed{3x-5y+1=0}3x−5y+1=0
si tu préfères, tu peux multiplier par -1 : −3x+5y−1=0\boxed {-3x+5y-1=0}−3x+5y−1=0si tu souhaites avoir l'équation sous la forme y=ax+by=ax+by=ax+b , tu isoles 5y5y5y puis yyy
5y=3x+15y=3x+15y=3x+1 d'où, en divisant par 3 :
y=35x+15\boxed{y=\dfrac{3}{5}x+\dfrac{1}{5}}y=53x+51Refais seul ces calculs.
Bon travail .
Je ne vois pas comment faire plus.
Et comment tu peux voir sur le schéma joint, l'équation trouvée est bien l'équation de la médiatrice de [AB], ensemble des points équidistants de A et B, c'est à dire tels que MA=MB
-
mtschoon dernière édition par

Comme déjà indiqué (au debut de ce topic), tu peux faire autrement :
Trouver les coordonnées de I mileu de [AB] et trouver, avec le produit scalaire, l'équation de la droite passant par I et perpendiculaire à (AB) :
AB→.IM→=0\overrightarrow{AB}.\overrightarrow{IM}=0AB.IM=0Tu peux faire les deux méthodes pour vérifier que trouves la même équation.
-
hugo.mt_22 dernière édition par
@mtschoon les propositions du dessus sont en rapport avec ceci: Dans le plan muni d'un repère orthonormé, soient les points A(2;−6) et B(−5;−3).
Donner une équation de la médiatrice du segment [AB][AB].
-
mtschoon dernière édition par mtschoon

@hugo-mt_22 , ce ne sont pas les mêmes données donc pas le même exercice.
Ouvre une nouvelle discussion si tu as besoin d'aide/vérification pour ce nouvel exercice.