Relation d'Al-kashi et produit scalaire

Bonjiur je ne comprend rien a cette exo serait il possible de m'aider svp

Soit ABC un triangle tel que AB = 3, AC = 5 et BC = 6. H est le pied de la hauteur
de ABC issue de A, et K celui de la hauteur issue de C.
1.
a) Calculer la valeur exacte de cos(ABC ), en précisant la formule utilisée.
b) Calculer −→B A.
−→BC, puis exprimer −→B A.
−→BC en fonction de B H. En déduire B H.
2.[texte du lien]([url du lien](![url du lien](url de l'image)))
Démontrer que BK ×B A = B H ×BC. En déduire BK.

@melvyn-oli , bonjour,

Je te joins une image.
Les cercles ne servent qu'à la construction.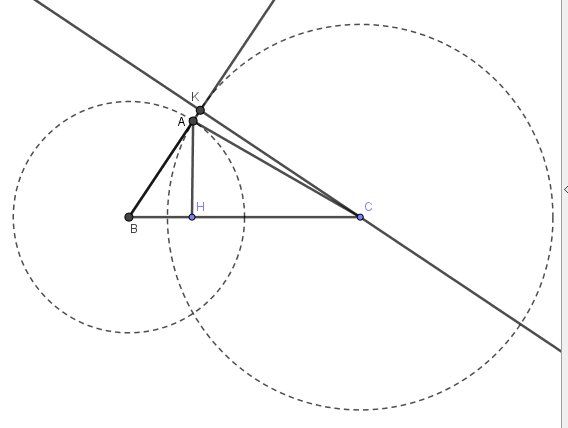

Piste pour démarrer,

a) Si tu connais la formule d'Al-Kashi

$b2=a2+c2−2ac×cos(ABC^)b^2=a^2+c^2-2ac \times cos(\widehat{ABC})$
Tu comptes :
$b = A C = 5$
$a = B C = 6$
$c = A B = 3$

Tu dois trouver, sauf erreur, $59\dfrac{5}{9}$ pour le cosinus.

b) $BA→.BC→=BA×BC×cos(ABC^)\overrightarrow{BA}.\overrightarrow{BC}=BA\times BC\times cos(\widehat{ABC})$

Tu as tout ce qu'il faut pour calculer.

Ensuite, comme par projection sur $(B C)$
$BA→.BC→=BH×BC\overrightarrow{BA}.\overrightarrow{BC}=BH\times BC$ , tu peux déduire $B H$

Essaie le faire cela et poursuis.

Reposte si tu as besoin d'aide et/ou vérifications.

Ce message a été supprimé !

@mtschoon tu peux me donner les reps stp car je trouve rien et la je suis desesperer

@melvyn-oli , il me semble que tu peux commencer par faire les calculs que je t'ai proposés et donner les résultats que tu as obtenus.

S'ils ne sont pas bons, tu auras des explications.

@mtschoon donc pour la a j'ai trouve 45.87 et la b 15.29

@melvyn-oli , bonjour,

Je regarde tes réponses,

Pour la a) , on te demande la valeur d'un cosinus.
Un cosinus est compris entre -1 et 1. Il ne peut pas valoir 45,87.

Avc la relation indiquée dans ma réponse précédente , tu peux écrire :
$52=62+32−2×6×3×cosABC^5^2=6^2+3^2-2\times 6\times 3\times cos\widehat{ABC}$
$25=45−36cosABC^25=45-36 cos\widehat{ABC}$
$36cosABC^=45−2536 cos\widehat{ABC}=45-25$
$36cosABC^=2036 cos\widehat{ABC}=20$
Tu termines en divisant par $36$ et en simplifiant.

b) Recompte aussi.