Bonjour je vous depande de l'aide car c'est exo son trop complique donc si cela ne vous genes pas de le faire et juste merci infiniment

Une entreprise de papeterie produit des stylos pouvant présenter deux défauts de
fabrication. Une étude statistique a montré que:
8 pour cent des stylos présentent le défaut A,
11 pour cent des stylos présentent le défaut B,
et 3 pour cent des stylos présentent les deux défauts.
a) On prélève un stylo au hasard dans la production, et on appelle X la variable
aléatoire qui donne le nombre de défauts du stylo choisi.
Déterminer la loi de probabilité de X.
b) Calculer l’espérance mathématique de X, et en donner une interprétation.

@melvyn-oli et me donner les resultats si je vous genes pas car sa fait 1 semaine chui decus je comprend rien dutout

Ce message a été supprimé !

@loicstephan desole de te gener mais qu'elle est la rep a et qu'elle est la rep b ?

Bonjour,

@loicstephan , l'énoncé est bien exact.

Tu peux voir que ta réponse est fausse car la somme des probabilités que tu utilises ne vaut pas 1.

Vu que tu proposes de l'aide, il faut que tu revois toute ta réponse, car X prend trois valeurs 0 , 1, 2 ( et non deux valeurs )

@mtschoon tu peux donner le resultats stp car je trouve pas

@melvyn-oli , bonjour,

Te donner les résultats ne te servira pas à grand'chose si tu ne les comprend pas...et en DS, tu ne sauras pas faire...

Ici, on évite, ce qui n'est pas toujours commode, de "donner les résultats"
On prèfère aider à les trouver

a)

$X = 2$ : deux défauts A et B : $p(X=2)=p(A∩B)=0.03p(X=2)=p(A\cap B)=\boxed{0.03}$

$X = 1$ : un seul défaut, c'est à dire défaut A sans B, ou bien défaut B sans A.

$\setminus B)=p(A \setminus (A\cap B))=p(A)-p(A\cap B)=0.08-0.03=0.05$

$\setminus A)$ se calcule avec la même démarche
A toi de faire.
Tu dois trouver
$\setminus A)=0.08$
Donc
$p(X=1)=0.05+0.08=0.13p(X=1)=0.05+0.08=\boxed{0.13}$

$P (X = 0)$ peut se déduire des deux calculs précédents.
$1 - 0.03 - 0.13 = 0.84$

On peut calculer autrement

$p(A∪B)=p(A)+p(B)−p(A∩B)=0.08+0.11−003=0.16p(A\cup B)=p(A)+p(B)-p(A\cap B)=0.08+0.11-003=0.16$

Donc $p(X=0)=1−0.16=0.84p(X=0)=1-0.16=\boxed{0.84}$

vérification : $0.03+0.13+0.84=1\boxed{0.03+0.13+0.84=1}$

Tu peux disposer ces résultats sous forme d'un tableau.

b) il te suffit d'appliquer la formule de ton cours pour calculer $E (X)$

Bonjour,

Pour celui qui préfère le visuel.

Diagramme de Venn (ou patate)

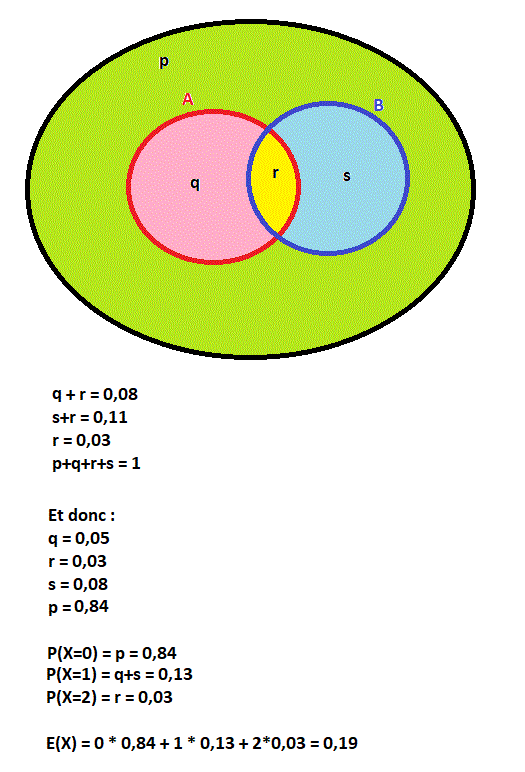
Sans titre.png

bonjour
juste pour comprendre d'avantage : que signifie P(B)?

@loicstephan , bonjour,

C'est vrai que les notations étaient usuelles, mais n'étaient pas explicitées

$p (B)$ : probabilité pour qu'une pièce ait le défaut B
$p (A)$ : probabilité pour qu'une pièce ait le défaut A
$p(A∩B)p(A\cap B)$ : probabilité pour qu'une pièce ait le défaut A ET le défaut B
$p(A∪B)p(A\cup B)$ : probabilité pour qu'une pièce ait le défaut A OU le défaut B (c'est à dire au moins un des deux défauts)

@mtschoon
on traduira donc $P (A / B)$ par probabilité pour qu'une pièce ait le défaut A sachant qu'elle ait le défaut B ?

Oui tout à fait @loicstephan (mais ça ne sert pas dans les questions posées).

parce qu"n realite cette probabilite est : $P(A/B)=P(A∩B)P(B)P(A/B)=\frac{P(A\cap B)}{P(B)}$

parce que ce qui intéresse est la probabilité d'avoir le défaut A sachant l'absence de défaut B
soit complémentaire à B

@loicstephan a dit dans

parce que ce qui intéresse est la probabilité d'avoir le défaut A sachant l'absence de défaut B
soit complémentaire à B

De quoi parles-tu ?

De la méthode pour trouver P(X=1) peut-être ?

Pour cela, comme indiqué , on cherche effectivement d'avoir un seul défaut, c'est à dire défaut A sans défaut B, ou bien défaut B sans défaut A.

REMARQUE
Il ne faut pas confondre la noatation P(A/B ) qui veut dire P(A sachant B) c'est une probabilité conditionnelle , avec p(A\B) qui veut dire "P(A moins B)" c'est à dire probabilité que la pièce ait le défaut A et n'ait pas le défaut B

Il n'y a pas de probabilité conditionnelle à chercher dans cet exercice.

J'espère que c'est clair pour toi (et pour @melvyn-oli )

@mtschoon a dit dans Bonjour je vous depande de l'aide car c'est exo son trop complique donc si cela ne vous genes pas de le faire et juste merci infiniment :

Il ne faut pas confondre la noatation P(A/B ) qui veut dire P(A sachant B) c'est une probabilité conditionnelle , avec p(A\B) qui veut dire "P(A moins B)" c'est à dire probabilité que la pièce ait le défaut A et n'ait pas le défaut B
Il n'y a pas de probabilité conditionnelle à chercher dans cet exercice.
J'espère que c'est clair pour toi (et pour @melvyn-oli )

Bonjour
Très clair c'est ca qui me perturbait merci @mtschoon

C'est parfait @loicstephan si tout est OK pour toi.
J'espère qu'il en est de même pour @melvyn-oli