Dm de math 1er spe mathematique

[ylime]

Bonjour,
J'aurais besoins de votre aide pour ce sujet svpppp
Seulement Partie B svppp

Lien supprimé par la modération du forum.

[ylime]

@ylime 𝐴𝐵𝐶 un triangle tel que 𝑏 = 7 , 𝐴 =𝜋/4
𝑒𝑡 𝐶=2𝜋/3 A et C sont des mesures d'angles

Déterminer une valeur approchée au dixième près des deux autres longueurs du triangle.

[Noemi]

@ylime Bonjour,

Utilise une des relations données dans la partie A.
Indique tes éléments de réponse.

[ylime]

@Noemi
Oui mais quelle relation la première ou deuxième ?

[Noemi]

@ylime

Tu as la mesure d'un côté et de deux angles, donc utilise la loi des sinus.
Indique tes calculs si tu souhaites une vérification.

[mtschoon]

Bonjour,

Un petit plus si besoin,@ylime

J'ignore de quoi parlait la partie A vu que tu ne l'as pas recopiée.

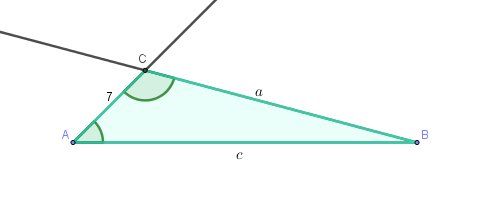
Les angles $\hat{A}$ et $\hat{C}$ sont remarquables donc tu connais leur sinus

$\hat{B}=\pi -(\frac{\pi }{4}+\frac{2\pi }{3})=\frac{\pi }{12}$

$sin\hat{B}=sin(\frac{\pi }{12})=sin(\frac{\pi }{3}-\frac{\pi }{4})$

Avec la formule de $sin(a-b)$ tu dois trouver

$sin(\frac{\pi }{12})=\frac{\sqrt{6}-\sqrt{2}}{4}$

Tu connais la distance $AC=b=7$

Avec la relation $\frac{a}{sin\hat{A}}=\frac{b}{sin\hat{B}}=\frac{c}{sin\hat{C}}$ , tu obtiens les réponses voulues.

Tu peux donner tes réponses si tu souhaites une vérification.