Produit scalaire dans le plan

[Traoré]

Bonjour j'ai exo que je ne comprends pas
On donne les points A(4;2) et B(-1;-3) et on note I le milieu du segment [AB]. Détermine et construis l'ensemble (C)des points M du plan tels que MA.MB=AB²

[mtschoon]

@Traoré , bonsoir,

Piste,

Tu dois avoir une propriété dans ton cours (que tu peux démontrer avec la relation de Chasles, si besoin)
$\overrightarrow{MA}.\overrightarrow{MB}=M{I}^2-\frac{A{B}^2}{4}$

Ainsi, la condition de l'énoncé s'écrit
$M{I}^2-\frac{A{B}^2}{4}=A{B}^2$

Tu isoles $M{I}^2$, tu calcules $A{B}^2$, et tu pourras déduire la valeur de $MI$ et la conclusion.

Reposte si besoin.

[Traoré]

@mtschoon bonsoir
MA.MB=(MI+IA).(MI+IB)=MI²+MI.IB+IA.MI+IA.IB=MI²+MI(IA+IB)-IA²=MI²-(AB/2)²=MI-AB²/4
Donc AB²=50 j'espère que ce que j'ai fait là c'est ça

[mtschoon]

@Traoré , bonjour

Il manque un carré à $MI$ à la fin de ton calcul (faute de frappe sans doute)

$A{B}^2=50$ est bon.

Tu peux donc déduire , comme indiqué pércédemment :
$M{I}^2=A{B}^2+\frac{A{B}^2}{4}$

Tu remplaces $A{B}^2$ par $50$ et tu dois trouver, sauf erreur,
$M{I}^2=\frac{250}{4}$, c'est à dire : $MI=\frac{5\sqrt{10}}{2}$

Conclusion:
I est fixe. Les points M sont à la distance $\frac{5\sqrt{10}}{2}$ de I

Tu en déduis l'ensemble (C) des points M.

Donne ta réponse si tu souhaite une vérification.

[Black-Jack]

Bonjour,

Alternative. (probablement pas celle attendue)

Soit M(X ; Y)
vect(MA) = (4-X;2-Y)
vect(MB) = (-1-X;-3-Y)
vect(MA).vect(MB) = (4-X)(-1-X)+(2-Y)(-3-Y) = 50
X²-3X+Y²+Y-10= 50
(X-3/2)² - 9/4 + (Y+1/2)² - 1/4 -10 + 60
(X-3/2)² + (Y+1/2)² = 62,5
Comme I(3/2 ; -1/2), le lieu des points M est un cercle centré sur I (point milieu de [AB]) et de rayon $=\sqrt{62,5}$

[mtschoon]

@Traoré ,

Je te laissais trouver la nature de (C), mais vu qu'elle t'a été donnée, je te joins l'illustration graphique $I(\frac{3}{2},-\frac{1}{2})$
$(C)$ cercle de centre $I$ et de rayon $R=\frac{5\sqrt{10}}{2}$
$R\approx 7.9$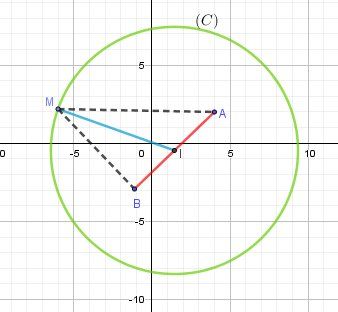

Bon travail.

[mtschoon]

J'espère que c'est clair pour toi.