problème de géométrie angles inscrits

bonjour!
je suis entrain d'aider mon petit frère et je tombe sur un exercice qui me semble manquer de donne alors je vous du coups je sais pas comment démarrer ca porte sur les angles et triangles inscrits

$C$ est un cercle de centre O et les points L M N P et Q sont des points de $C$ telle que le montre la figure ci-dessous.
on donne l'angle PMQ=132 degre
determiner les mesures des angle suivants: PLQ, POQ, PNQ
comment vous faire parvenir la figure le scan d'ennce etant interdit

@loicstephan Bonjour,

Tu transmets le scan que de la figure.

@Noemi

@loicstephan

Bizarre la position du point O centre du cercle.

Utilise le Théorème :
La mesure d'un angle inscrit dans un cercle est égale à la moitié de la mesure de l'angle au centre qui intercepte le même arc.
Si deux angles inscrits interceptent le même arc, alors ils ont la même mesure.

Voir le cours : https://www.mathforu.com/troisieme/theoremes-de-l-angle-au-centre-des-angles-inscrits/

Bonjour,

Comme le dit @Noemi , le point O est très bizarre...et on ne sait pas trop où est le point M...

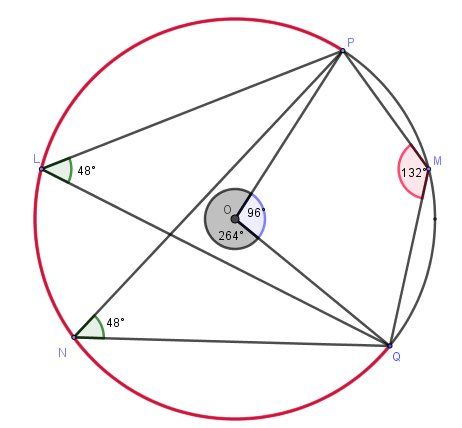
Je viens de faire une figure en interprétant ce que je crois "comprendre"...

@loicstephan , il faudra dire si elle correspond vraiment à la figure de départ (?), mais de toute façon, je pense que tu as tout ce qu'il faut pour arriver à faire les calculs.

@loicstephan c'est un peu flou mais ca devrait aller !

exactement bizarre je crois que la figure de @mtschoon est la figure a comprendre !

le problème c'est de trouver 96! comment vous trouver 96 parce que le reste se déduit

@loicstephan

Regarde le cours que j'ai indiqué.
L'angle au centre est égal au double de l'angle inscrit.
L'angle PMQ = 132 ° donc l'angle POQ qu'intercepte le même arc vaut ....
.....

@loicstephan

Tant mieux si mon schéma est bon...

L'arc qui intercepte l'angle inscrit $PMQ^\widehat{PMQ}$ est en rouge sur mon schéma (Je l'avais mis de la même couleur que l'angle inscrit $PMQ^\widehat{PMQ}$ ) .

L'angle au centre correspondant est en gris sombre sur mon schéma donc il vaut le double de 132°, c'est à dire 264°.

Tu dois pouvoir déduire le 96° facilement, puis les angles de 48° en conséquence.

@mtschoon
PMQ et POQ sont il interceptés par le même arc de cercle?

Si un quadrilatère convexe est inscrit dans un cercle, alors ses angles opposés sont supplémentaires.(avec cette propriété je détermine $48 = 180 - 132$ mesure de l'ange inscrit .
l'angle inscrit étant la moitie de l'angle au centre intercepté par le même arc de cercle alors il vaut $2 * 48 = 96$ )

@loicstephan

La démonstration est correcte.

Pour les angles interceptés par le même arc de cercle regarde la réponse de mtschoon.

@loicstephan

PMQ et POQ sont il interceptés par le même arc de cercle?

Si tu parles de l'angle inscrit en rouge (132°), de l'angle au centre en gris foncé (264°) : ils interceptent le même arc d'extrèmités P et Q colorié en rouge.

L'explication que tu donnes est bonne (tout dépend de ce que contient le cours de ton petit frère).

@mtschoon
oui c'est vue merci @Noemi @mtschoon

@loicstephan ,

OK
Bon travail pour ton petit frère.