Produits scalaire exercice
-
JJeans yao dernière édition par
Bonjour j'ai un exercice que je n'arrive pas affaire la deuxième question
ABC est un triangle tel que AB=3 AC=4 et AB.AC=6. On désigne par H le projeté orthogonal de C sur la droite (AB)- calcul Ah
- Détermine une mesure en degré de l'angle BAC
J'ai réussi à faire la première question
Comme H est le projeté de C sur (AB) alors AB.AC=AB×AH
6=3AH donc AH =2 mais je n'arrive pas à faire la deuxième question
-
mtschoon dernière édition par mtschoon

@Jeans-yao , bonjour,
Je pense que tu as voulu écrire : AB→.AC→=6\overrightarrow{AB}.\overrightarrow{AC}=6AB.AC=6
Oui pour ta première réponse : AH=2AH=2AH=2
Pour répondre la second question, tu as le choix
Dans le triangle AHC, tu peux écrire :
cos(BAC^)=AHACcos(\widehat{BAC})=\dfrac{AH}{AC}cos(BAC)=ACAH
Tu peux ainsi trouver le cosinus, puis l'angle.Tu peux faire autrement en utilisant la définition du produit scalaire
AB→.AC→=AB×AC×cos(BAC^)\overrightarrow{AB}.\overrightarrow{AC}=AB\times AC\times cos(\widehat{BAC})AB.AC=AB×AC×cos(BAC)Tu trouveras évidemment la même réponse.
Tu peux donner ta réponse pour vérification si tu le souhaites.
-
mtschoon dernière édition par mtschoon

Illustration graphique.
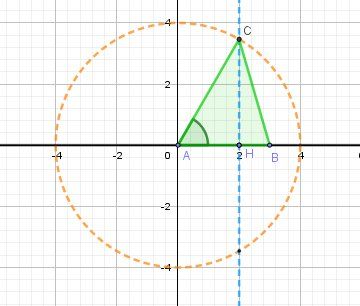
-
JJeans yao dernière édition par
@mtschoon bonsoir
Donc la mesure de l'angle va être 60°
-
mtschoon dernière édition par

@Jeans-yao ,
Oui, c'est tout à fait exact.
Le cosinus vaut 12\dfrac{1}{2}21, d'où 60° pour l'angle.