SVP j ai besoin d aide dans un exercice de nombres complexes

Bonjour
j ai des difficultés a répondre aux questions suivantes
résoudre dans C l équation (E): 1+2z+2z^2+2z^3+2z^3+2z^4+z^5=0
-le plan complexe est rapporte a un repere orthonorme direct (o,u,v)
on appelle A0,A1,A2,A3,A4 les points a affixes respectives 1,z1,z1^2,z2^2,z3^2,z4^2
soit H le point d intersection de la droite (A1A4) et l axe (o,u)
montrer que zH=cos2pi/5

@Mariem-jabloun , bonjour,

Je regarde ta question 1) : 1+2z+2z^2+2z^3+2z^3+2z^4+z^5=0

Bizarre : 2z^3 est écrit deux fois...

Faute de frappe ?

Piste pour le cas où il s'agit de
$1+2z+2z2+2z3+2z4+z5=0\boxed{1+2z+2z^2+2z^3+2z^4+z^5=0}$

Solution évidente : $z=−1\boxed{z=-1}$

Tu peux mettre $(z + 1)$ en facteur
Sauf erreur, l'équation peut s'écrire :
$z+1)(z^4+z^3+z^2+z+1)=0$

Il faut résoudre $1+z+z^2+z^3+z^4=0$
Utilise la formule de la somme des 5 premiers termes de la suite géométrique de premier terme 1 et de raison $z$
Tu t'assures que $1$ n'est pas solution de l'équation.
$1−z51−z=0\dfrac{1-z^5}{1-z}=0$ <=> $1-z^5=0$ <=> $z^5=1$
$z$ est donc racine 5ième de 1 ( sauf $1$ )
$z=e2ikπ5\boxed{z=e^{\dfrac{2ik\pi}{5}}}$ avec $k$ prenant les valeurs $1, 2, 3, 4$
Tu exprimes ces solutions sous la forme qui te convient

Tu obtiens ainsi les 5 solutions de l'équation.

Vérifie que la piste donnée corresponde à l'équation que tu voulais écrire.

Pour la question 2, je trouve ton énoncé pas assez précis pour pouvoir y répondre...détaille les notations utilisées.

@mtschoon
oui j ai répondu a cette question
mais pour la deuxième question je pense que z1,z2...et z4 sont les solutions de cette équation
ce n est pas précis dans l énoncé
si non pourriez vous me donner la méthode pour trouver l affixe d un point sachant qu il est l intersection de deux droites

Bonjour,

"on appelle A0,A1,A2,A3,A4 les points a affixes respectives 1,z1,z1^2,z2^2,z3^2,z4^2"

Il y a une erreur d'énoncé ... on donne 5 points pour 6 affixes.

@Mariem-jabloun ,

Comme déjà dit, la seconde question n'est pas claire.
Les données auraient dû être explicitées.
De plus, il y a (encore) une anomalie.

Tu écris :
on appelle A0,A1,A2,A3,A4 les points a affixes respectives 1,z1,z1^2,z2^2,z3^2,z4^2
Cela fait 5 points et 6 affixes !

Je suppose que z1 est de trop (???) ce n'est qu'une supposition...
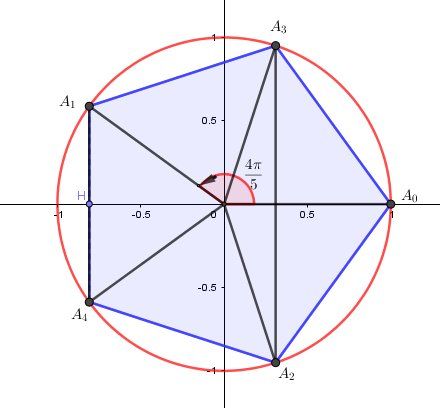
Ainsi, $A_0,.., A_4$ auraient pour affixes les carrés des solutions de l'équation (E)

Avec l'ordre que j'ai donné à la première question :

$A_0 : (-1)^2=1$

$A1:(e2iπ5)2=e4iπ5A_1 : \biggr(e^{\dfrac{2i\pi}{5}}\biggr)^2=e^{\dfrac{4i\pi}{5}}$

$A2:(e4iπ5)2=e8iπ5=e−2iπ5A_2 : \biggr(e^{\dfrac{4i\pi}{5}}\biggr)^2=e^{\dfrac{8i\pi}{5}}=e^{-\dfrac{2i\pi}{5}}$

$A3:(e6iπ5)2=e12iπ5=e2iπ5A_3 : \biggr(e^{\dfrac{6i\pi}{5}}\biggr)^2=e^{\dfrac{12i\pi}{5}}=e^{\dfrac{2i\pi}{5}}$

$A4:(e8iπ5)2=e16iπ5=e−4iπ5A_4 : \biggr(e^{\dfrac{8i\pi}{5}}\biggr)^2=e^{\dfrac{16i\pi}{5}}=e^{-\dfrac{4i\pi}{5}}$

Tu peux placer ces points de module 1 (donc sur le cercle trigonométrique) dans le plan complexe.
$A_1$ et $A_4$ sont symétriques par rapport à l'axe des réels (axe des abscisses);
Idem pour $A_2$ et $A_3$

L'affixe de H est donc l'abscisse commune de $A_1$ et $A_4$
Elle vaut $cos4π5cos\dfrac{4\pi}{5}$

Ce n'est pas ce que tu indiques dans ton énoncé...

Pour obtenir $cos2π5cos\dfrac{2\pi}{5}$ il aurait fallu que H soit à l'intersection de $A_2A_3)$ avec l'axe des réels.

Remarque : vu que tu dis que les valeurs de $z_1,z_2,z_3,z_4$ ne sont pas indiquées dans ton énoncé (ce qui est fort surprenant), tu peux échanger les notations entre $A_1, A_4)$ et $A_2,A_3)$ pour obtenir la réponse proposée $cos2π5cos\dfrac{2\pi}{5}$ .

En bref, vérifie ton énoncé et adapte.

@Mariem-jabloun ,

Illustration correspondant aux propositions données