démonstration pour 3 eme
-
Lloicstephan dernière édition par
bonsoir
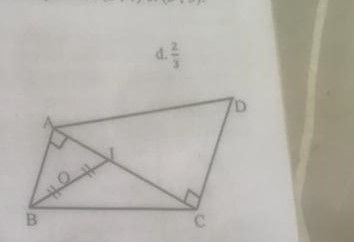
encore un exercice pour petit frère qui bloqueABCDABCDABCD est un quadrilatère III est un point de AC tel qu'en centimètre AI=2AI=2AI=2 BI=4BI=4BI=4 les droite (AB)(AB)(AB) et (CD)(CD)(CD) sont perpendiculaires a la droite ACACAC et le point OOO désigne le milieux du segment BIBIBI
-
justifie que (AB)(AB)(AB) et (CD)(CD)(CD) (Pas de soucis)
-
calcule ABABAB ( par le théorème de Pythagore sauf erreur je calcule ABABAB)
-
calcule le cos angle ABIABIABI (pas de soucis)
4)nomme le centre du cercle circonscrit au triangle AIBAIBAIB et détermine une mesure en degré de l'angle AOIAOIAOI ( c'est ici que je bloque)
-
-
Lloicstephan dernière édition par loicstephan

v 
-
@loicstephan Bonjour,
Attention, le multipost est interdit sur ce forum. L'autre post va être supprimé.
Pour la mesure de l'angle, quelle est la nature des triangles AOB et AOC ?
-
Lloicstephan dernière édition par
@Noemi
triangle équilatéral et rectangle peut être je ne perçoit pas trop s'il y a un cercle inscrit je me dit on déduire des propriétés y associées
-
C'est un cercle circonscrit, quels sont les segments qui ont pour mesure celle du rayon du cercle ?
-
mtschoon dernière édition par mtschoon

Bonjour,
ABCD est -il convexe? concave? croisé ?
Si tu as un schéma, ce serait bien de le donner pour que les consultants puissent comprendre clairement.
Merci.Remarque : il y a bien deux images données, mais visiblement elles ne s'ouvrent pas.
-
mtschoon dernière édition par mtschoon

Bonjour,
@loicstephan ( ou plutôt son frère )
Un schéma possible (sans certitude)
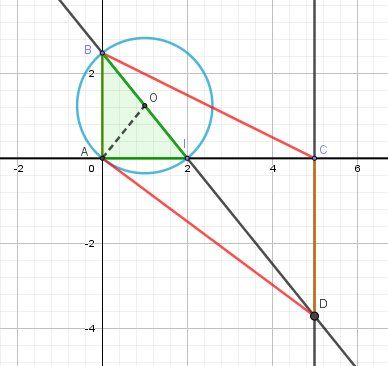
(AB)//(CD)(AB)//(CD)(AB)//(CD)
IB2=AB2+AI2IB^2=AB^2+AI^2IB2=AB2+AI2 d'où AB2=16−4=12AB^2=16-4=12AB2=16−4=12 d'où AB=23AB=2\sqrt3AB=23
cosABI^=ABBIcos\widehat{ABI}=\dfrac{AB}{BI}cosABI=BIAB Tu comptes.
Tu déduis ABI^\widehat{ABI}ABILe triangle AIBAIBAIB étant rectangle en AAA, le centre du cercle circonscrit au triangle a pour centre OOO , milieu de [BI][BI][BI]
L'angle au centre AOI^\widehat{AOI}AOI est, par théorème, le double de ABI^\widehat{ABI}ABI.
-
Lloicstephan dernière édition par
@Noemi
BI
-
Lloicstephan dernière édition par
-
mtschoon dernière édition par mtschoon

@loicstephan , bonjour,
Merci pour ton schéma.
Je viens de vérifier si les pistes indiquées avec le schéma "possible" (sans certitude) sont encore valables avec ton schéma réel : c'est tout bon.
-
Lloicstephan dernière édition par
@mtschoon merci
-
Lloicstephan dernière édition par
@Noemi merci
-
mtschoon dernière édition par

De rien @loicstephan .
Nous faisons le mieux possible.