Devoir fonctions réciproques

Bonsoir j'ai besoin d'aide, il faut déterminer algébriquement et graphiquement la fonction suivante :

F: R--> R : X--> 1/(x-2)²
J'ai déjà fait ma c.e j'ai trouvé le domaine suivant: domf= R(2) donc il y a une AV en 2 et je pense une AH en 0.
C'est quand il faut inverser le x et le y afin de démontrer si ou non il y a injectivite que je rencontre des difficultés.

Merci à ceux qui prendront le temps de répondre.

@__mnl__elm__ , bonsoir,

Oui pour ce que tu proposes pour asymptote horizontale et verticale.
Dans le schéma, la courbe est en bleu, AV est en rouge et AH est l'axe des abscisses.

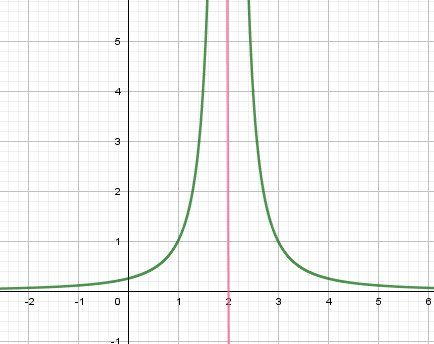
Pour l'injectivité : c'est NON

Pour dire"non", un exemple sufffit
f(1)=f(3)=1
1 et 3 ont la même image par f donc f non injective.

@mtschoon d'accord je vois, mais j'ai tout de même une question. L'ensemble image se trouve tout le temps grâce au graphique ou il y a une autre technique ?

@__mnl__elm__ ,

Pour trouver l'ensemble image, le mieux est d'étudier les variations de la fonction (ensemble de définition, de dérivabilité, dérivée, son signe, variations de la fonction et limites aux bornes de l'ensemble de définition) et de résumer tout cela dans le tableau de variation de la fonction.

La représentation graphique en est l'illustration.