Exercice Probabilités

[yasmi16]

Bonsoir,
Je vous écris au sujet de l’exercice suivant :
Le bateau ivre arrive à un croisement où le fleuve se sépare en trois. Il va prendre une des trois directions avec les probabilités 1/6, 1/3 et 1/2 Dans chaque direction, les probabilités de parvenir entier jusqu'à la mer sont respectivement 1/3, 2/3 et 7/9
Le lendemain, il s'écrase au bas d'une cataracte.
Calculer la probabilité qu'il ait pris la deuxième direction.

J’ai déjà du mal avec la compréhension de l’énoncé, déjà les premières proba je sais pas vraiment à quoi elles correspondent.
Et je n’arrive pas à voir le raisonnement que je pourrais avoir.
Merci d’avance
Bonne soirée

[mtschoon]

@yasmi16 , bonjour,

Je te conseille un arbre probabiliste pour éclairer ton exercice (en faisant abstraction des indications inutiles...)

En voici un

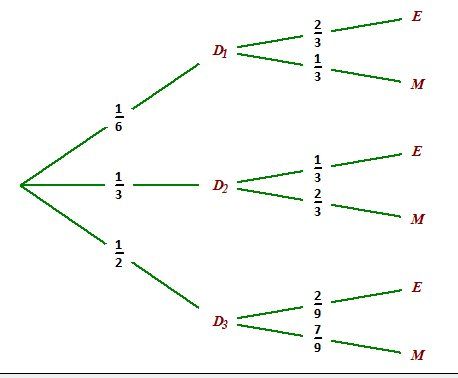
Dans cet arbre,
$D_1,D_2,D_3$ correspondent aux trois directions.
$M$ est l'évènement "le bateau arrive entier à la mer"
$E$ évènement contraire de $M$ est l'évènement "le bateau s'écrase".

Lorsque tu as compris les probabilités indiquées, les calculs se déduisent (revois ton cours)

$p(E)=(\frac{1}{6})(\frac{2}{3})+(\frac{1}{3})(\frac{1}{3})+(\frac{1}{2})(\frac{2}{9})$ Tu comptes

L'énoncé te demande de calculer la probabilité pour que le bateau ait pris la deuxième direction, sachant qu'il s'écrase (probabilité conditionnelle)
$p_E(D_2)=\frac{p(D_2\cap E)}{p(E)}$=$\frac{(\frac{1}{3})(\frac{1}{3})}{p(E)}$ Tu comptes.

Revois tout ça de près et reposte si besoin.

[yasmi16]

@mtschoon
Bonjour,
Merci pour votre aide c’est plus clair en effet. C’est une proba conditionnelle donc théorème de bayes.
Merci passez une bonne journée

[mtschoon]

De tien @yasmi16 et bonnes probabilités !