Exo sur les équations cartesienne

Bonjour,es ce possible d'avoir un peu d aide pour cet exos svp

Soit (D) la droite d équation 3x +y +2=0 et A le point de (D) d'abscisse -1
Déterminer une équation cartésienne du cercle passant par l origine et tangent à la droite (D) en A

@jordanmezui , bonjour,

Ici la politesse n'est pas une option...
Il faudra y penser une autre fois.

Je te mets un schéma pour éclairer la démarche.

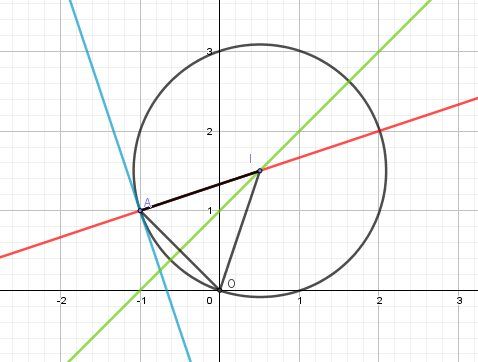
cercle tangentjpg.jpg

Une piste possible,

La droite (D) d'équation $y = - 3 x - 2$ est en bleu.

Tu peux trouver l'équation de la droite passant par A et perpendiculaire à (D) . Elle est en rouge.
Après calcul, elle a pour équation $y=13x+43y=\dfrac{1}{3}x+\dfrac{4}{3}$

Tu peux chercher l'équation de la médiatrice de [AO] qui est en vert sur le schéma.

L'intersection de ces 2 droites (rouge et verte) est le point I dont tu peux trouver les coordonnées et qui sera le centre du cercle cherché, vu que tu auras ainsi $(IA)⊥(D)(IA)\perp (D)$ et $I A = I O$

Tu pourras déduire l'équation du cercle

Tu peux donner tes réponses si tu souhaites une vérification.

@mtschoon j ai trouvé comme réponses :
_I(7/2;5/2)
IO=74/4
L' équation du cercle est (x+7/2)^2 +(y+5/2)^2

@jordanmezui IO^2=74/4
Excusez-moi pour l'erreur

@jordanmezui , tes résultats sont à revoir.
Si tu avais regardé le graphique , tu aurais pu constater que les coodonnées de I que tu donnes ne sont pas exacts.

Pour l'équation de la médiatrice de [AO], tu dois trouver $y = x + 1$

En résolvant le système composé par les deux équations de droites (rouge et verte) tu dois trouver $I(12,32)I(\dfrac{1}{2}, \dfrac{3}{2})$

Rappel pour l'équation d'un cercle de centre $I (a, b)$ et de rayon $R$ :
$x-a)^2+(y-b)^2=R^2$

Donc, revois tout ça et reposte si besoin.

@mtschoon avec quel outil tu as tracé ton schéma ?

Mathématiques terminale

@eleve__1 , bonsoir,

Tu comptes faire ta publicité partout ? ? ?

Mon schéma est fait avec Geogebra (logiciel gratuit, que tout matheux connait )