Équation cartesienne

Re : Exo sur les équations cartesienne
Re-bonjour, excusez mais c est pour un autre exercice
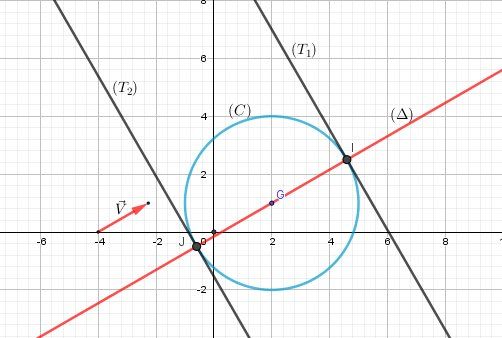
Soit (C)le cercle de centre g(2;1) et de rayon 3.
1.Determiner les points de ce cercle où la tangente admet pour vecteur normal v(√3;1).
2.Ecrire une équation de chacune de ces tangente .

@jordanmezui , bonjour,

Schéma pour éclairer ton exercice

Revois bien ton cours sur équations de cercles et droites.

Pistes pour démarrer,

$(C)$ a pour équation $x−2)2+(y−1)2=9\boxed{x-2)^2+(y-1)^2=9}$

$V→\overrightarrow V$ est vecteur normal aux tangentes cherchées, donc $V→\overrightarrow V$ est vecteur directeur de la droite $(Δ)(\Delta)$ passant par $G$ et perpendiculaires à ces tangentes.

Tu cherches l'équation de $(Δ)(\Delta)$ de la forme $A x + B y + C = 0$
Vu que $V→\overrightarrow V$ a pour coordonnées $(3,1)(\sqrt 3,1)$ , tu obtiens :
$−B=3-B=\sqrt 3$ et $A = 1$ donc $B=−3B=-\sqrt 3$ et $A = 1$

L'équation de $(Δ)(\Delta)$ peut s'écrire : $x−3y+C=0x-\sqrt 3y+C=0$

Vu qu'elle passe par $G$ , en remplaçant x et y par les coordonnées de $G$ tu obtiens : $C=3−2C=\sqrt 3-2$

Equation de $(Δ)(\Delta)$ : $x−3y+3−2=0\boxed{x-\sqrt 3y+\sqrt 3-2=0}$

En résolvant le système composé par les deux équations encadrées, tu obtiendras les coordonnées de $I$ et $J$

Regarde tout ça de près et essaie de poursuivre.
Reposte si besoin.