Probabilités conditionnelles

Bonjour voici un sujet qui me pose des difficultés :
Trois urnes U1, U2 et U3 contiennent des boules rouges et des boules vertes en nombres différents
On note N1 (respectivement N2 et N3) le nombre total de boules dans l’urne U1 (respectivement U2 et U3).
On note N = N1 + N2 + N3
La proportion de boules rouges est p1 (respectivement p2 et p3) dans l’urne U1 (respectivement U2 et U3) Les réponses aux questions qui suivent seront données en fonction des données p1, p2, p3, N1, N2 et N3 Rappel : une proportion est comprise entre 0 et 1

On tire au hasard le numéro de l’urne dans laquelle on prend au hasard une boule. Quelle est la probabilité qu’elle soit rouge ?
On réunit toutes les boules des trois urnes dans une seule urne. La probabilité de tirer une boule rouge est-elle la même que précédemment ?

Pour la 1) j'ai trouvé 1/3(p1+p2+p3) mais pour la 2 je coince. Une petite aide svp ?

Bonsoir @Mimi25000 ,

Pour la 2) on peut commencer par prendre un exemple , prenons 200 boules vertes dans les urnes U1 et U2 ,et pour U3 seulement une boule rouge en réunissant en une urne pense-tu avoir la même probabilité ?

Après pour obtenir une probabilité on peut poser n1(n2 et n3) le nombre de boule rouge tel que p1=n1/N1(resp. p2,p3)
On réunit l'ensemble des boules dans une seul urne soit Ptotal = (n1+n2+n3)/N

Bonjour,

C'est jamais très clair un énoncé de probabilité...

@Mimi25000 , voilà comment je "vois" la première question.

Pour l'éclairer , je te conseille un arbre probabiliste.

Je t'en joins un avec des notations assez "parlantes", mais demande si tu ne les comprends pas.

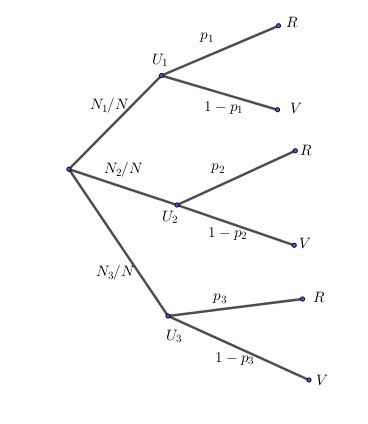
Les probabilités indiquées sur l'arbre sont relatives aux nombres de boules.
( c'est pour cela que le 1/3 que tu utilises ne convient pas car il ne tient pas compte du nombre de boules et c'est ce qui est nécessaire pour les calculs )
Si il y avait $N_1=N_2=N_3$ , le 1/3 conviendrait.

Dans $U_1$ , il y a $N_1$ boules .
Le nombre total de boules est $N$
La probabilité de choisir une boule de $U_1$ est $N_1/N$
Idem nour $U_2$ et $U_3$
$R$ est la probabilité de choisir une boule rouge,
$V$ est la probabilité de choisir une boule verte;

En utilisant les propriétés de l'arbre, la probabilité de choisir une boule rouge est donc :
$p(R)=[(N1/N)×p1]+[(N2/N)×p2]+[(N3/N)×p3]p(R)=[(N_1/N)\times p_1]+[(N_2/N)\times p_2]+[(N_3/N)\times p_3]$

Pour la seconde question, c'est plus simple, vu qu'il y a une seule urne $U$
En utilisant la même démarche, c'est "trivial"
La probabilité de choisir une boule de $U$ est $N1+N2+N3N=1\dfrac{N_1+N_2+N_3}{N}=1$
La probabilité de choisir une boule rouge est
$p_1+p_2+p_3$

Réfléchis à tout ça et tire la conclusion.

@mtschoon merci
par contre je ne comprends pas que le choix de l'urne au hasard dépendent des boules qu'il y a à l'intérieur...On choisit une urne au hasard et ensuite on tire une boule.

@Mimi25000 , je comprends très bien ta question, mais il faut faire avec l'énoncé...
Vu que l'on te donne les nombres de boules contenues dans les urnes, si tu n'en tiens pas compte, ces nombres ne serviraient à rien...
C'est pour cela que je t'ai proposé un calcul en tenant compte des nombres de boules ; ça donne un sens à l'énoncé.

Tu peux penser que, en choisissant au hasard une urne , on choisit par la même (sans le savoir), une proportion de boules contenues dans l'urne choisie.

Si les nombres de boules dans les urnes n'avaient pas été donnés, tu aurais pris $1 / 3, 1 / 3, 1 / 3$ pour le choix des urnes comme tu l'as fait.

Comme déjà dit, c'est rarement clair un énoncé de probabilité... il faudrait être dans la tête de celui qui l'a écrit.

A toi de décider sur l'interprétation que tu souhaites.