variables aléatoires discrétes
-
Mariem Mansour dernière édition par Noemi
s'il vous plait, comment on a trouvé ce résultat ?
Scans supprimés par la modération du site.
-
@Mariem-Mansour Bonjour,
Le scan de l'énoncé de l'exercice est interdit sur ce forum. Seuls les scans de schémas, graphiques ou figures sont autorisés.
Ecris l'énoncé, indique la question qui te pose problème et tu obtiendras des pistes de résolution.Le scan va être supprimé.
-
Mariem Mansour dernière édition par Mariem Mansour
@Mariem-Mansour a dit dans variables aléatoires discrétes :
s'il vous plait, comment on a trouvé ce résultat ?
s'il vous plait, comment on a trouvé ce résultat ?
On considère une urne contenant N boules numérotés de 1 à N:- Un joueur prélève simultanement n boules de l'urne (1 <= n <= N). Soit X le plus grand numéro
de boules tirées et Y le plus petit numéro. Déterminer la loi de X et la loi de Y:
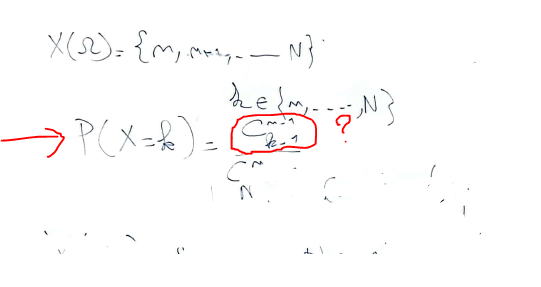
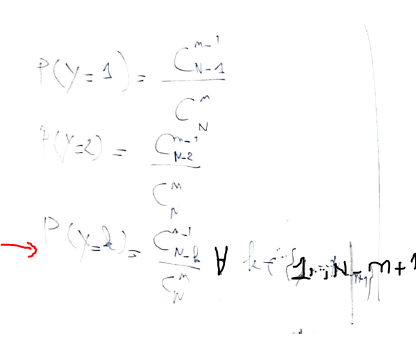
- Un joueur prélève simultanement n boules de l'urne (1 <= n <= N). Soit X le plus grand numéro
-
mtschoon dernière édition par mtschoon

Bonjour,
@Mariem-Mansour , bien sûr ce n'est pas l'énoncé, mais ton "brouillon" scanné n'était pas utile.
Je te donne quelques pistes pour la variable XXX
Boules numérotées : 1,2,...,k−1‾,k,k+1,....,N\underline{1,2,...,k-1},k,k+1, ....,N1,2,...,k−1,k,k+1,....,N
Soir n≤Nn\le Nn≤N
Le nombre de façons de choisir nnn boules parmi N est CNn\boxed{C_N^n}CNn
Parmi ces nnn boules, soit kkk la plus grande valeur.
Nécessairement k≤N\boxed{k\le N}k≤N
Cela revient à choisir la boule kkk (une façon) et (n−1)(n-1)(n−1) autres boules parmi les (k−1)(k-1)(k−1) boules dont le numéro est inférieur à kkk .(partie soulignée de la liste des boules)Condition (pour pouvoir choisir (n−1)(n-1)(n−1) boules parmi (k−1)(k-1)(k−1) boules:
n−1≤k−1n-1\le k-1n−1≤k−1 c'est à dire n≤kn\le kn≤k, d'où n≤k≤N\boxed{n\le k\le N}n≤k≤NLe nombre de façons de choisir (n−1)(n-1)(n−1) autres boules parmi les (k−1)(k-1)(k−1) boules est : Ck−1n−1\boxed{C_{k-1}^{n-1}}Ck−1n−1
Conclusion :
P(X=k)=Ck−1n−1CNn\boxed{P(X=k)=\dfrac{C_{k-1}^{n-1}}{C_N^n}}P(X=k)=CNnCk−1n−1Tu peux faire le même type de raisonnement pour YYY.